/Szkoła średnia/Zadania maturalne/Matura 2010
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 20 marca 2010 Czas pracy: 180 minut
Wyznacz wszystkie wartości parametru 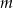 , dla których równanie
, dla których równanie 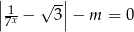 ma dwa pierwiastki, których iloczyn jest ujemny.
ma dwa pierwiastki, których iloczyn jest ujemny.
Rozwiąż układ równań 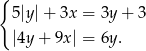
W trójkącie prostokątnym 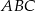 przyprostokątne mają długości
przyprostokątne mają długości 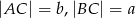 , a wysokość opuszczona z wierzchołka kąta prostego ma długość
, a wysokość opuszczona z wierzchołka kąta prostego ma długość 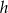 .
.
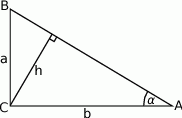
Wykaż, że jeżeli 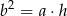 to
to 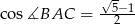 .
.
Z miejscowości 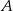 i
i 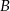 , które są odległe o 58,5 km wyruszyły jednocześnie ku sobie dwa samochody. Pierwszy samochód w ciągu pierwszej minuty jechał ze średnią prędkością 30 km/h, a w ciągu każdej następnej minuty pokonywał drogę o 0,25 km dłuższą, niż w ciągu poprzedniej minuty. Drugi samochód przez pierwsze 6 minut przejechał 21 kilometrów, a potem jechał ze stałą prędkością 150 km/h. Oblicz po ilu minutach nastąpi spotkanie samochodów.
, które są odległe o 58,5 km wyruszyły jednocześnie ku sobie dwa samochody. Pierwszy samochód w ciągu pierwszej minuty jechał ze średnią prędkością 30 km/h, a w ciągu każdej następnej minuty pokonywał drogę o 0,25 km dłuższą, niż w ciągu poprzedniej minuty. Drugi samochód przez pierwsze 6 minut przejechał 21 kilometrów, a potem jechał ze stałą prędkością 150 km/h. Oblicz po ilu minutach nastąpi spotkanie samochodów.
Ciąg 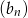 jest nieskończonym ciągiem liczb dodatnich, a ciąg
jest nieskończonym ciągiem liczb dodatnich, a ciąg 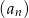 spełnia warunek
spełnia warunek
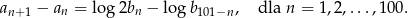
Oblicz 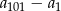 .
.
Ze zbioru 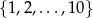 losujemy dwie różne liczby
losujemy dwie różne liczby  i
i 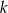 . Oblicz prawdopodobieństwo, że
. Oblicz prawdopodobieństwo, że
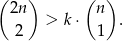
Okrąg o środku 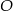 jest wpisany w trójkąt
jest wpisany w trójkąt 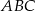 , gdzie
, gdzie 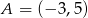 . Wiedząc, że okrąg ten jest styczny do boków
. Wiedząc, że okrąg ten jest styczny do boków 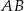 i
i 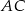 odpowiednio w punktach
odpowiednio w punktach 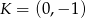 i
i 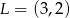 oblicz długość odcinka
oblicz długość odcinka 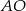 .
.
Wyznacz wartość parametru 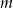 , dla którego równanie
, dla którego równanie
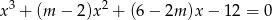
ma trzy pierwiastki 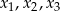 spełniające warunki
spełniające warunki 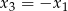 oraz
oraz 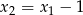 .
.
Trapez prostokątny 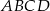 o podstawach
o podstawach 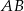 i
i 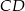 jest opisany na okręgu o promieniu
jest opisany na okręgu o promieniu  .
.
- Wykaż, że
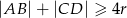 .
. - Wiedząc, że pole trapezu jest równe 4 wykaż, że
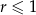 .
.
Na płaskiej powierzchni położono trzy kule 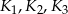 , każda o promieniu 2 tak, że kule
, każda o promieniu 2 tak, że kule 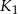 i
i 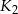 są styczne w punkcie
są styczne w punkcie 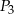 , kule
, kule 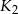 i
i 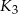 są styczne w punkcie
są styczne w punkcie 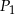 , a kule
, a kule 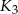 i
i 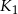 są styczne w punkcie
są styczne w punkcie 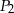 . Następnie położono na tych kulach kulę
. Następnie położono na tych kulach kulę 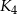 o promieniu 3, która jest styczna do kul
o promieniu 3, która jest styczna do kul 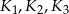 odpowiednio w punktach
odpowiednio w punktach 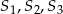 .
.
- Uzasadnij, że odcinki
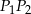 i
i 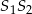 są równoległe.
są równoległe. - Oblicz obwód trapezu
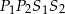 .
.
Wykaż, że dla dowolnych liczb rzeczywistych 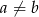 oraz
oraz 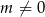 równanie
równanie
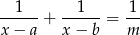
ma dwa różne rozwiązania.

