/Szkoła średnia/Zadania maturalne/Matura 2007/Matura
Egzamin Maturalny
z Matematyki poziom podstawowy 14 maja 2007 Czas pracy: 120 minut
Znajdź wzór funkcji kwadratowej 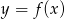 , której wykresem jest parabola o wierzchołku
, której wykresem jest parabola o wierzchołku 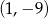 przechodząca przez punkt o współrzędnych
przechodząca przez punkt o współrzędnych 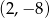 . Otrzymaną funkcję przedstaw w postaci kanonicznej. Oblicz jej miejsca zerowe i naszkicuj wykres.
. Otrzymaną funkcję przedstaw w postaci kanonicznej. Oblicz jej miejsca zerowe i naszkicuj wykres.
Wysokość prowizji, którą klient płaci w pewnym biurze maklerskim przy każdej zawieranej transakcji kupna lub sprzedaży akcji jest uzależniona od wartości transakcji. Zależność ta została przedstawiona w tabeli:
| Wartość transakcji | Wysokość prowizji |
| do 500 zł | 15 zł |
| od 500,01 zł do 3000 zł | 2% wartości transakcji + 5 zł |
| od 3000,01 zł do 8000 zł | 1,5% wartości transakcji + 20 zł |
| od 8000,01 zł do 15000 zł | 1% wartości transakcji + 60 zł |
| powyżej 15000 zł | 0,7% wartości transakcji + 105 zł |
Klient zakupił za pośrednictwem tego biura maklerskiego 530 akcji w cenie 25 zł za jedną akcję. Po roku sprzedał wszystkie kupione akcje po 45 zł za jedną sztukę. Oblicz, ile zarobił na tych transakcjach po uwzględnieniu prowizji, które zapłacił.
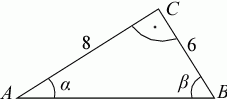
Korzystając z danych przedstawionych na rysunku, oblicz wartość wyrażenia:
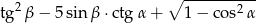
Samochód przebył w pewnym czasie 210 km. Gdyby jechał ze średnią prędkością o 10 km/h większą, to czas przejazdu skróciłby się o pół godziny. Oblicz, z jaką średnią prędkością jechał ten samochód.
Dany jest ciąg arytmetyczny 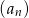 , gdzie
, gdzie 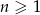 . Wiadomo, że dla każdego
. Wiadomo, że dla każdego 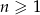 suma
suma  początkowych wyrazów
początkowych wyrazów 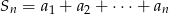 wyraża się wzorem:
wyraża się wzorem: 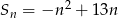 .
.
- Wyznacz wzór na
 –ty wyraz ciągu
–ty wyraz ciągu 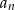 .
. - Oblicz
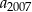 .
. - Wyznacz liczbę
 , dla której
, dla której 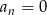 . .
. .
Dany jest wielomian 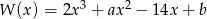 .
.
- Dla
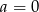 i
i 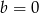 otrzymamy wielomian
otrzymamy wielomian 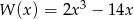 . Rozwiąż równanie
. Rozwiąż równanie 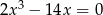 .
. - Dobierz wartości
 i
i 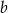 tak, aby wielomian
tak, aby wielomian 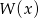 był podzielny jednocześnie przez
był podzielny jednocześnie przez 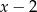 oraz
oraz 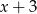 .
.
Dany jest punkt 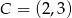 i prosta o równaniu
i prosta o równaniu 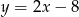 będąca symetralną odcinka
będąca symetralną odcinka 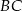 . Wyznacz współrzędne punktu
. Wyznacz współrzędne punktu 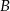 . Wykonaj obliczenia uzasadniające odpowiedź.
. Wykonaj obliczenia uzasadniające odpowiedź.
Na stole leżało 14 banknotów: 2 banknoty o nominale 100 zł, 2 banknoty o nominale 50 zł i 10 banknotów o nominale 20 zł. Wiatr zdmuchnął na podłogę 5 banknotów. Oblicz prawdopodobieństwo tego, że na podłodze leży dokładnie 130 zł. Odpowiedź podaj w postaci ułamka nieskracalnego.
Oblicz pole czworokąta wypukłego 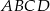 , w którym kąty wewnętrzne mają odpowiednio miary:
, w którym kąty wewnętrzne mają odpowiednio miary: 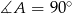 ,
, 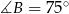 ,
, 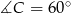 ,
, 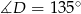 , a boki
, a boki 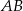 i
i 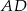 mają długość 3 cm. Sporządź rysunek pomocniczy.
mają długość 3 cm. Sporządź rysunek pomocniczy.
Dany jest graniastosłup czworokątny prosty 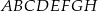 o podstawach
o podstawach 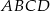 i
i 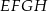 oraz krawędziach bocznych
oraz krawędziach bocznych 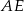 ,
, 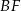 ,
, 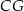 ,
, 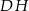 . Podstawa
. Podstawa 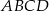 graniastosłupa jest rombem o boku długości 8 cm i kątach ostrych
graniastosłupa jest rombem o boku długości 8 cm i kątach ostrych 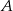 i
i 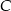 o mierze
o mierze 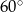 . Przekątna graniastosłupa
. Przekątna graniastosłupa 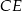 jest nachylona do płaszczyzny podstawy pod kątem
jest nachylona do płaszczyzny podstawy pod kątem 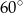 . Sporządź rysunek pomocniczy i zaznacz na nim wymienione w zadaniu kąty. Oblicz objętość tego graniastosłupa.
. Sporządź rysunek pomocniczy i zaznacz na nim wymienione w zadaniu kąty. Oblicz objętość tego graniastosłupa.
Dany jest rosnący ciąg geometryczny 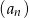 dla
dla 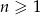 , w którym
, w którym 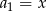 ,
, 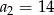 ,
, 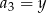 . Oblicz
. Oblicz  oraz
oraz 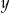 , jeżeli wiadomo, że
, jeżeli wiadomo, że 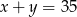 .
.

