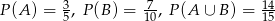Zadanie nr 1778544
Ze zbioru 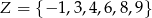 losujemy bez zwracania liczby
losujemy bez zwracania liczby  i
i 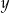 . Oblicz prawdopodobieństwa zdarzeń:
. Oblicz prawdopodobieństwa zdarzeń: 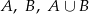 jeśli:
jeśli:
A – suma wylosowanych liczb jest nieparzysta;
B – wylosowane liczby spełniają warunek: 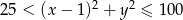 .
.
Rozwiązanie
Jeżeli za zdarzenia elementarne przyjmiemy pary (uporządkowane) wylosowanych liczb to mamy
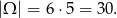
Jeżeli suma wylosowanych liczb ma być nieparzysta, to jedna z nich musi być parzysta, a druga nieparzysta. Jest
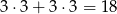
takich par (osobno liczymy pary, gdy pierwsza liczba jest parzysta, i gdy druga liczba jest parzysta). Zatem
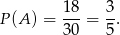
Spróbujmy teraz rozszyfrować zdarzenie 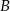 . Podany warunek oznacza, że punkt
. Podany warunek oznacza, że punkt 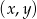 leży w pierścieniu kołowym między okręgami o środku
leży w pierścieniu kołowym między okręgami o środku 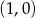 i promieniach 5 i 10 (i może być na zewnętrznym, a na wewnętrznym nie). Jeżeli sobie to naszkicujemy, to możemy wypisać pasujące pary.
i promieniach 5 i 10 (i może być na zewnętrznym, a na wewnętrznym nie). Jeżeli sobie to naszkicujemy, to możemy wypisać pasujące pary.
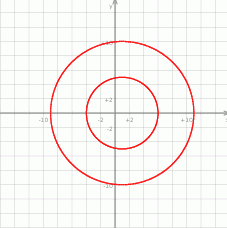
My jednak tego nie zrobimy, zamiast tego wypiszemy pary złe, czyli sprzyjające zdarzeniu 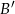 – jak się okaże jest ich znacznie mniej (niektóre punkty sprawdzamy podstawiając do wzoru).
– jak się okaże jest ich znacznie mniej (niektóre punkty sprawdzamy podstawiając do wzoru).
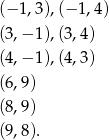
Zatem
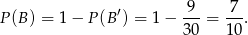
Aby obliczyć prawdopodobieństwo 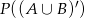 trzeba ze zdarzeń przeciwnych do
trzeba ze zdarzeń przeciwnych do 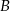 wyrzucić te, w których suma liczb jest nieparzysta (bo te są w
wyrzucić te, w których suma liczb jest nieparzysta (bo te są w 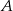 ). Pozostaną zatem
). Pozostaną zatem
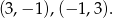
Prawdopodobieństwo jest więc równe
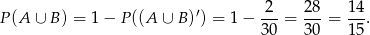
Odpowiedź: