/Szkoła średnia/Prawdopodobieństwo/Z definicji/Zbiory liczb

Zadanie nr 2456258

Dodaj do ulubionych
Dodaj do rozwiązanych

Ze zbioru 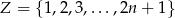Z = { 1,2,3,...,2n + 1} , gdzie 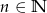n ∈ N wylosowano równocześnie dwie liczby. Wyznacz n , tak aby prawdopodobieństwo wylosowania liczb, których suma jest liczbą nieparzystą było większe od 713- .

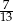Rozwiązanie

Zauważmy, że liczby nieparzyste w danym zbiorze to

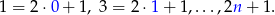
1 = 2 ⋅0 + 1, 3 = 2 ⋅1+ 1,...,2n + 1.

Jest ich więc 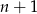n + 1 . Podobnie liczby parzyste to

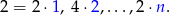
2 = 2⋅1 , 4 ⋅2,...,2 ⋅n.

Jest ich więc n .

Jeżeli za zdarzenia elementarne przyjmiemy nieuporządkowane pary wylosowanych liczb, to

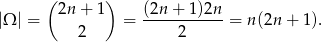
( ) 2n + 1 (2n-+-1)2n- |Ω | = 2 = 2 = n(2n + 1 ).

Jeżeli suma wylosowanych liczb ma być nieparzysta, to jedna z nich musi być nieparzysta a druga parzysta. Mamy więc

(n+ 1)n

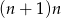
zdarzeń sprzyjających (wybieramy jedną liczbę parzystą i jedną nieparzystą). Zatem

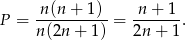
n(n + 1) n + 1 P = ---------- = -------. n(2n + 1) 2n + 1

Mamy do rozwiązania nierówność

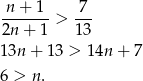
n + 1 7 ------- > --- 2n + 1 13 13n + 13 > 14n + 7 6 > n.

 
Odpowiedź: n ∈ { 1,2,3,4,5}

Wersja PDF