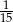/Szkoła średnia/Prawdopodobieństwo/Z definicji/Zbiory liczb

Zadanie nr 6076129

Dodaj do ulubionych
Dodaj do rozwiązanych

W urnie jest 15 kartek, ponumerowanych liczbami od 1 do 15. Wyciągamy 5 kartek bez zwracania. Jakie jest prawdopodobieństwo, że numer trzeciej kartki jest liczbą podzielną przez 3 i jednocześnie numer piątej kartki jest liczbą podzielną przez 5?

Rozwiązanie

Sposób I

Przyjmijmy, że zdarzenia elementarne to uporządkowane ciągi 5–cio elementowe wylosowanych numerów. Zatem

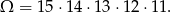
Ω = 15 ⋅14 ⋅13 ⋅12 ⋅11.

W zdarzeniach sprzyjających mamy 3 możliwości na numer 5–tej kartki (5, 10 lub 15). Mamy teraz dwie możliwe sytuacje.

Jeżeli na piątym miejscu jest 15, to na trzecie miejsce mamy 4 możliwości (3, 6, 9 lub 12). Na pozostałe miejsca mamy odpowiednio 13, 12 i 11 możliwości.

Jeżeli na piątym miejscu jest 10 lub 5, to na trzecie miejsce mamy 5 możliwości (3, 6, 9, 12 lub 15). Na pozostałe miejsca mamy odpowiednio 13, 12 i 11 możliwości.

Razem mamy więc

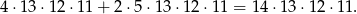
4⋅13 ⋅12 ⋅11 + 2 ⋅5⋅ 13⋅ 12⋅1 1 = 14 ⋅13 ⋅12⋅ 11.

Szukane prawdopodobieństwo wynosi więc

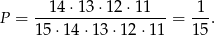
--14-⋅13-⋅12-⋅11-- 1-- P = 15 ⋅14 ⋅13 ⋅12 ⋅11 = 15.

Sposób II

Tym razem za zdarzenia elementarne przyjmijmy wszystkie uporządkowane ciągi 15 kartek. Mamy zatem

|Ω | = 1 5!.

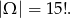
Zdarzenia sprzyjające to takie, w których na 3 miejscu jest: 3, 6, 9, 12 lub 15, a na 5 miejscu jest: 5, 10 lub 15. Możliwości wypełnienia tych miejsc jest

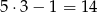
5 ⋅3 − 1 = 14

(pierwszą z liczb wybieramy spośród 5 możliwości, a drugą spośród 3 możliwości i na koniec odejmujemy jeden zły wybór, gdy na obu miejscach wybraliśmy 15). Po ustaleniu liczb na 3 i 5 miejscu, pozostałe liczby możemy umieścić na 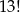13! sposobów. Interesujące na prawdopodobieństwo jest więc równe

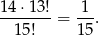
14 ⋅13! 1 ------- = --. 15 ! 15

 
Odpowiedź: 115

Wersja PDF