Zadanie nr 6965729
Ze zbioru 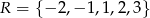 losujemy najpierw jedną liczbę i oznaczamy ją jako
losujemy najpierw jedną liczbę i oznaczamy ją jako  . Następnie z pozostałych liczb losujemy drugą liczbę i oznaczamy ją jako
. Następnie z pozostałych liczb losujemy drugą liczbę i oznaczamy ją jako 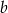 . Liczby
. Liczby  i
i 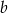 są współczynnikami funkcji kwadratowej
są współczynnikami funkcji kwadratowej 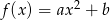 . Oblicz prawdopodobieństwo zdarzenia:
. Oblicz prawdopodobieństwo zdarzenia:
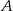 – funkcja
– funkcja 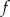 jest malejąca w zbiorze
jest malejąca w zbiorze 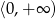 ,
, 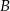 – funkcja
– funkcja 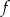 ma dwa różne miejsca zerowe.
ma dwa różne miejsca zerowe.
Rozwiązanie
Możliwości wybrania liczb  i
i 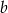 jest
jest
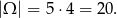
Wykresem funkcji 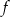 jest parabola o wierzchołku w punkcie
jest parabola o wierzchołku w punkcie 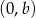 .
.
- Jeżeli funkcja
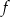 ma być malejąca w przedziale
ma być malejąca w przedziale 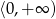 , to ramiona paraboli będącej jej wykresem muszą być skierowane w dół, czyli musi być
, to ramiona paraboli będącej jej wykresem muszą być skierowane w dół, czyli musi być 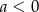 . Takich par jest
. Takich par jest 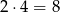
(liczbę
 możemy wybrać na 2 sposoby i potem wybieramy liczbę
możemy wybrać na 2 sposoby i potem wybieramy liczbę 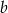 z pozostałych liczb). Interesujące nas prawdopodobieństwo jest więc równe
z pozostałych liczb). Interesujące nas prawdopodobieństwo jest więc równe 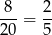
Odpowiedź:
- Jeżeli wykresem funkcji jest parabola o ramionach skierowanych w górę (czyli
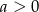 ), to jej wierzchołek musi być poniżej osi
), to jej wierzchołek musi być poniżej osi 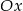 , czyli musi być
, czyli musi być 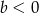 . Takich par jest
. Takich par jest 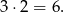
Jeżeli natomiast ramiona paraboli są skierowane w dół (czyli
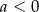 ), to jej wierzchołek musi być powyżej osi
), to jej wierzchołek musi być powyżej osi 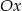 (czyli
(czyli 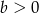 ). Takich par jest
). Takich par jest 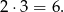
Interesujące nas prawdopodobieństwo jest więc równe
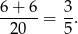
Odpowiedź:

