/Szkoła średnia/Prawdopodobieństwo/Z definicji/Zbiory liczb

Zadanie nr 7721149

Dodaj do ulubionych
Dodaj do rozwiązanych

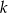Z ustalonego zbioru n liczb rzeczywistych losujemy kolejno k liczb, otrzymując ciąg różnowartościowy 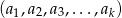(a1,a2,a3,...,ak) . Zakładając, że 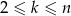2 ≤ k ≤ n , oblicz prawdopodobieństwo, że ten ciąg nie jest ciągiem rosnącym.

Rozwiązanie

Sposób I

Ciąg 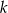k elementowy ze zbioru n elementowego można wybrać na

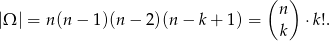
(n ) |Ω | = n(n − 1)(n − 2 )(n− k+ 1) = ⋅k!. k

sposobów. Zamiast liczyć szukane prawdopodobieństwo 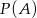P(A ) , policzmy prawdopodobieństwo zdarzenia przeciwnego 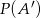P (A ′) , tzn. zdarzenia w którym ciąg jest rosnący. Ile jest takich zdarzeń? – tyle ile podzbiorów 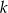k elementowych w zbiorze n elementowym (bo po wybraniu podzbioru kolejność liczba jest już ustalona). Mamy zatem

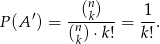
(n) P (A′) = -n-k--- = -1. (k) ⋅k! k!

Szukane prawdopodobieństwo wynosi więc

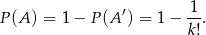
P(A ) = 1 − P (A ′) = 1 − 1-. k!

Sposób II

Tak jak poprzednio liczymy prawdopodobieństwo zdarzenia przeciwnego 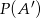′ P (A ) . Możemy wszystkie zdarzenia elementarne (wszystko jedno ile ich jest) pogrupować w zbiory zdarzeń, które odpowiadają permutacjom jednego ciągu. W każdej takiej grupie jest 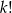k! zdarzeń i jest dokładnie jedno zdarzenie sprzyjające 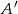A ′ , zatem

′ 1- P (A ) = k!

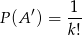
(można myśleć, że jest to wzór na prawdopodobieństwo całkowite, ale lepiej myśleć, że to zdrowy rozsądek).  
Odpowiedź: -1 1 − k!

Wersja PDF