/Szkoła średnia/Prawdopodobieństwo/Z definicji/Zbiory liczb

Zadanie nr 7828777

Dodaj do ulubionych
Dodaj do rozwiązanych

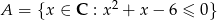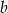Ze zbioru 2 A = {x ∈ C : x + x− 6 ≤ 0} losujemy 2 liczby a i b bez zwracania i tworzymy funkcję 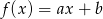f (x) = ax + b . Oblicz prawdopodobieństwo otrzymania funkcji, która nie ma miejsc zerowych.

Rozwiązanie

Na początek rozszyfrujmy zbiór 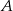A .

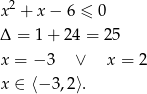
2 x + x − 6 ≤ 0 Δ = 1+ 24 = 25 x = − 3 ∨ x = 2 x ∈ ⟨− 3,2⟩.

Zatem

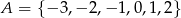
A = {− 3,− 2,− 1,0,1,2}

i

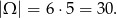
|Ω | = 6 ⋅5 = 30 .

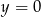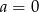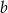Aby funkcja nie miała miejsc zerowych musi być stała i różna od y = 0 . Musimy zatem mieć a = 0 i b dowolne (różne od 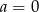a = 0 ). Prawdopodobieństwo wynosi

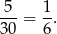
5 1 ---= -. 30 6

 
Odpowiedź: 1 6

Wersja PDF