Zadanie nr 7861512
Ze zbioru 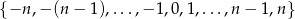 , gdzie
, gdzie 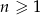 losujemy dwie liczby (mogą się powtarzać). Oblicz jakie jest prawdopodobieństwo, że suma wartości bezwzględnych wylosowanych liczb jest nie większa niż
losujemy dwie liczby (mogą się powtarzać). Oblicz jakie jest prawdopodobieństwo, że suma wartości bezwzględnych wylosowanych liczb jest nie większa niż  .
.
Rozwiązanie
Ponieważ losujemy ze zwracaniem wygodnie będzie nam myśleć o parach 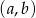 . W podanym zbiorze jest
. W podanym zbiorze jest 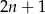 liczb, więc
liczb, więc
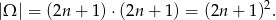
Pozostało teraz policzyć ile jest par 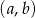 spełniających podany warunek.
spełniających podany warunek.
Sposób I
Policzmy ile jest takich par, patrząc na kolejne możliwe wartości  .
.
Jeżeli 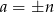 to musi być
to musi być 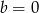 , czyli mamy dwie pary.
, czyli mamy dwie pary.
Jeżeli 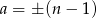 to musi być
to musi być 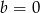 lub
lub 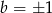 (bo suma wartości bezwzględnych ma być nie większa od
(bo suma wartości bezwzględnych ma być nie większa od  ), czyli mamy sześć takich par (mamy 2 możliwości wyboru znaku na pierwszej współrzędnej i 3 możliwości wyboru drugiej współrzędnej).
), czyli mamy sześć takich par (mamy 2 możliwości wyboru znaku na pierwszej współrzędnej i 3 możliwości wyboru drugiej współrzędnej).
Jeżeli 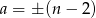 to musi być
to musi być 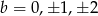 . Daje to nam 10 par.
. Daje to nam 10 par.
Jeżeli 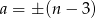 to musi być
to musi być 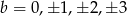 . Daje nam to
. Daje nam to
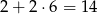
możliwości (najpierw liczymy pary z zerem, potem wybieramy znak przy pierwszej współrzędnej i wybieramy drugą liczbę).
Powinno być już widać co jest grane, ale sprawdźmy ogólnie dla 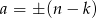 .
.
Jeżeli 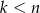 , to
, to 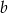 może być jedną z liczb
może być jedną z liczb 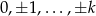 . Daje nam to
. Daje nam to
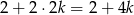
możliwości (pierwsza dwójka to pary z zerem, dalej mamy wybór znaku przy  i
i 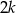 możliwości wyboru
możliwości wyboru 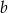 ).
).
Popatrzmy jeszcze osobno co się dzieje dla 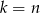 . Wtedy
. Wtedy 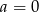 i
i 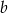 jest dowolną liczbą z danego zbioru, więc jest
jest dowolną liczbą z danego zbioru, więc jest 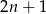 takich par.
takich par.
W sumie mamy więc
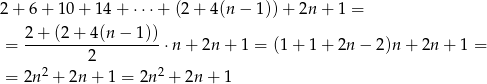
zdarzeń sprzyjających. Po drodze skorzystaliśmy ze wzoru na sumę kolejnych wyrazów ciągu arytmetycznego.
Szukane prawdopodobieństwo jest więc równe
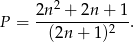
Sposób II
Największy problem w powyższym rachunku to zabawa z możliwymi znakami wylosowanych liczb. Można jednak łatwo się tego problemu pozbyć, jeżeli będziemy liczyć trochę sprytniej. Pomysł jest taki, żeby policzyć pary z dodatnimi liczbami, a potem uwzględnić możliwe wybory znaków. Aby się nie pogubić rozważmy niektóre sytuacje osobno.
Jest jedna para z dwoma zerami: 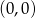 .
.
Jeżeli dokładnie jedna z liczb  lub
lub 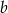 jest zero, to drugą liczbę możemy wybrać na
jest zero, to drugą liczbę możemy wybrać na 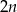 sposobów (nie może być 0!). Musimy jednak tę liczbę możliwości pomnożyć przez 2, co odpowiada wyborowi, która współrzędna ma być równa 0. W sumie jest więc
sposobów (nie może być 0!). Musimy jednak tę liczbę możliwości pomnożyć przez 2, co odpowiada wyborowi, która współrzędna ma być równa 0. W sumie jest więc 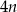 par z jednym zerem.
par z jednym zerem.
Całą resztę jest już dość łatwo policzyć. Będziemy liczyć pary 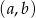 gdzie
gdzie 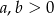 , a potem wynik przemnożymy przez 4 (co odpowiada możliwym zmianom znaków). Liczbę
, a potem wynik przemnożymy przez 4 (co odpowiada możliwym zmianom znaków). Liczbę  możemy wybrać na
możemy wybrać na  sposobów (od 1 do
sposobów (od 1 do  ). Przy ustalonej liczbie
). Przy ustalonej liczbie  , liczba
, liczba 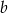 może być jedną z liczb
może być jedną z liczb 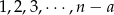 .
.
Pozostało teraz przesumować te liczby zmieniając  od 1 do
od 1 do 
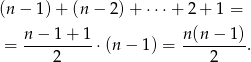
Na koniec mnożymy wynik przez 4 i mamy 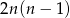 par z niezerowymi współrzędnymi. W sumie jest więc
par z niezerowymi współrzędnymi. W sumie jest więc
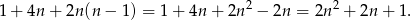
Prawdopodobieństwo liczymy jak w poprzednim sposobie.
Odpowiedź: