Zadanie nr 8634502
Ze zbioru 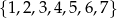 losujemy dwa razy po jednej liczbie bez zwracania. Z wylosowanych liczb tworzymy liczbę dwucyfrową w następujący sposób: mniejsza z wylosowanych liczb jest cyfrą jedności, a większa cyfrą dziesiątek utworzonej liczby. Oblicz prawdopodobieństwo otrzymania liczby podzielnej przez 7.
losujemy dwa razy po jednej liczbie bez zwracania. Z wylosowanych liczb tworzymy liczbę dwucyfrową w następujący sposób: mniejsza z wylosowanych liczb jest cyfrą jedności, a większa cyfrą dziesiątek utworzonej liczby. Oblicz prawdopodobieństwo otrzymania liczby podzielnej przez 7.
Rozwiązanie
Sposób I
Za zdarzenia elementarne przyjmijmy pary wylosowanych liczb. Zatem
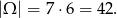
W zdarzeniach sprzyjających otrzymana liczba musi dzielić się przez 7, czyli być jedną z liczb 14, 21, 35, 42, 56, 63. Zauważmy jednak, że w utworzonych liczbach cyfra dziesiątek jest zawsze większa od cyfry jedności. Skraca to powyższą listę możliwości do: 21, 42, 63. Wystarczy teraz zauważyć, że każdy z tych wyników odpowiada dwóm zdarzeniom sprzyjającym:
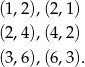
Prawdopodobieństwo jest więc równe
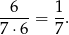
Sposób II
Tym razem za zdarzenia elementarne przyjmijmy nieuporządkowane pary wylosowanych liczb, czyli dwuelementowe podzbiory zbioru 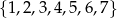 . Mamy więc
. Mamy więc
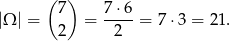
Jak w poprzednim sposobie ustalamy, że utworzona liczba będzie podzielna przez 7 wtedy i tylko wtedy, gdy będzie jedną z liczb: 21, 42, 63. Są więc dokładnie trzy zdarzenia sprzyjające (bo teraz ignorujemy kolejność losowania). Prawdopodobieństwo jest więc równe
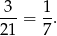
Odpowiedź: