Zadanie nr 8874389
Spośród liczb 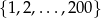 wybieramy losowo bez zwracania dwie liczby. Oblicz prawdopodobieństwa
wybieramy losowo bez zwracania dwie liczby. Oblicz prawdopodobieństwa 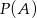 i
i 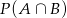 , gdzie
, gdzie 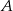 i
i 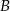 są następującymi zdarzeniami:
są następującymi zdarzeniami: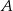 – druga z wylosowanych liczb jest mniejsza od 2;
– druga z wylosowanych liczb jest mniejsza od 2;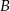 – różnica wylosowanych liczb jest podzielna przez 3.
– różnica wylosowanych liczb jest podzielna przez 3.
Rozwiązanie
Przyjmijmy, że zdarzenia elementarne to pary wylosowanych liczb. Zatem
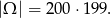
Zdarzenia sprzyjające do 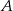 to takie, gdzie na drugim miejscu jest 1. Jest ich zatem 199 i mamy
to takie, gdzie na drugim miejscu jest 1. Jest ich zatem 199 i mamy
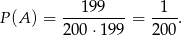
Zdarzenia sprzyjające 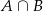 to takie, gdzie na drugim miejscu mamy 1, a na pierwszym liczbę postaci
to takie, gdzie na drugim miejscu mamy 1, a na pierwszym liczbę postaci 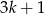 (żeby różnica dzieliła się przez 3). Policzmy ile jest liczb tej postaci w danym przedziale (nie liczymy 1, bo losujemy bez zwracania).
(żeby różnica dzieliła się przez 3). Policzmy ile jest liczb tej postaci w danym przedziale (nie liczymy 1, bo losujemy bez zwracania).
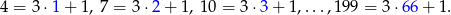
Widać, że jest 66 takich liczb i prawdopodobieństwo wynosi
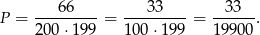
Odpowiedź: