Zadanie nr 8999576
Liczbę naturalną nazywamy palindromiczną, jeżeli nie zmienia się po zapisaniu jej cyfr w odwrotnej kolejności. Liczbami palindromicznymi są np. liczby 5, 33, 1123211. Liczby 10, 3230 nie są palindromiczne.
- Oblicz prawdopodobieństwo, że losowo wybrana liczba siedmiocyfrowa jest liczbą palindromiczną.
- Oblicz prawdopodobieństwo, że suma dwóch losowo wybranych liczb dwucyfrowych jest nieparzystą dwucyfrową liczbą palindromiczną.
Rozwiązanie
- Liczby siedmiocyfrowe to
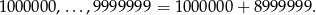
Jest ich zatem
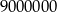 .
. 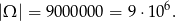
Można też było to wyliczyć: pierwszą cyfrę możemy wybrać na 9 sposobów (nie może być 0), a każdą kolejną na 10.
Policzmy ile jest liczb palindromicznych. Pierwszą (a więc jednocześnie ostatnią) cyfrę możemy wybrać na 9 sposobów (nie może być to 0). Drugą, trzecią i czwartą możemy wybrać na 10 sposobów. Pozostałe cyfry są już jednoznacznie wyznaczone. Mamy zatem
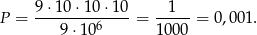
Odpowiedź: 0,001 - Za zdarzenia elementarne przyjmijmy nieuporządkowane pary wylosowanych liczb. Ponieważ jest 90 liczb dwucyfrowych to
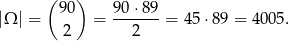
Wszystkie nieparzyste dwucyfrowe liczby palindromiczne to 11, 33, 55, 77, 99. Aby policzyć zdarzenia sprzyjające ustalmy, że
 jest mniejszą z wylosowanych liczb (nie mogą być równe bo suma jest nieparzysta). Mamy następujące możliwości
jest mniejszą z wylosowanych liczb (nie mogą być równe bo suma jest nieparzysta). Mamy następujące możliwości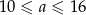 , wtedy drugą liczbę możemy dobrać na 4 sposoby:
, wtedy drugą liczbę możemy dobrać na 4 sposoby: 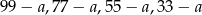 .
.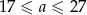 , wtedy drugą liczbę możemy dobrać na 3 sposoby:
, wtedy drugą liczbę możemy dobrać na 3 sposoby: 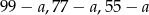 .
.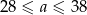 , wtedy drugą liczbę możemy dobrać na 2 sposoby:
, wtedy drugą liczbę możemy dobrać na 2 sposoby: 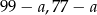 .
.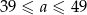 , wtedy drugą liczbę możemy dobrać na 1 sposób:
, wtedy drugą liczbę możemy dobrać na 1 sposób: 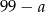 .
.
Jest zatem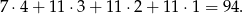
zdarzeń sprzyjających. Stąd
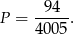
Odpowiedź: