Zadanie nr 9342657
Mamy trzy pudełka: w pierwszym znajduje się 6 kul ponumerowanych kolejnymi liczbami od 1 do 6, w drugim – 4 kule ponumerowane kolejnymi liczbami od 1 do 4, a w trzecim – 5 kul ponumerowanych kolejnymi liczbami od 1 do 5. Losujemy po jednej kuli z każdego pudełka i tworzymy liczbę trzycyfrową w ten sposób, że numer kuli wylosowanej z pierwszego pudełka jest cyfrą setek, numer kuli wylosowanej z drugiego pudełka jest cyfrą dziesiątek, a numer kuli wylosowanej z trzeciego – cyfrą jedności tej liczby. Oblicz prawdopodobieństwo, że utworzona liczba jest podzielna przez 4.
Rozwiązanie
Trzy kule z danych pudełek możemy wybrać na 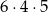 sposobów.
sposobów.
Liczba jest podzielna przez 4, gdy przez 4 podzielna jest liczba utworzona z dwóch ostatnich cyfr tej liczby. Liczba utworzona według warunków zadania będzie więc podzielna przez 4, gdy będzie się kończyć jedną z końcówek:
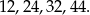
Cyfra setek może być dowolna, więc można utworzyć
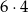
liczb podzielnych przez 4. Prawdopodobieństwo jest więc równe
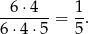
Odpowiedź: