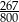/Szkoła średnia/Prawdopodobieństwo/Z definicji/Zbiory liczb

Zadanie nr 9649275

Dodaj do ulubionych
Dodaj do rozwiązanych

Ze zbioru 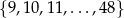{9,10,11 ,...,4 8} losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że suma wylosowanych liczb będzie podzielna przez 3.

Rozwiązanie

W danym zbiorze jest

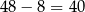
48 − 8 = 40

liczb, więc zdarzeń elementarnych jest

40⋅4 0.

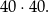
Aby obliczyć liczbę zdarzeń sprzyjających zauważmy, że liczby w danym zbiorze możemy podzielić na trzy grupy:

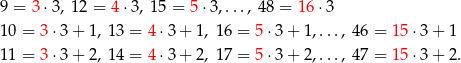
9 = 3⋅3, 12 = 4 ⋅3, 15 = 5 ⋅3,..., 48 = 16 ⋅3 10 = 3⋅3 + 1 , 13 = 4⋅3 + 1, 16 = 5 ⋅3 + 1,..., 46 = 15 ⋅3 + 1 11 = 3⋅3 + 2 , 14 = 4⋅3 + 2, 17 = 5 ⋅3 + 2,..., 47 = 15 ⋅3 + 2.

W pierwszej grupie jest 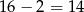16 − 2 = 14 liczb, a dwóch pozostałych po 13 liczb.

Zauważmy teraz, że jeżeli pierwszą liczbę wylosujemy z pierwszej grupy (czyli podzielną przez 3), to druga też musi być podzielna przez 3 (żeby suma była podzielna przez 3). Jest więc

14 ⋅14

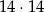
takich zdarzeń. Jeżeli natomiast pierwsza liczba jest z drugiej grupy (czyli daje resztę 1 przy dzieleniu przez 3), to druga liczba musi być z trzeciej grupy. Analogicznie, gdy pierwsza liczba jest z trzeciej grupy, to druga musi być z pierwszej grupy. W sumie jest więc

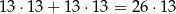
13⋅ 13+ 13⋅ 13 = 26 ⋅13

takich zdarzeń i interesujące nas prawdopodobieństwo jest równe

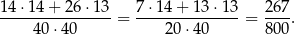
14⋅ 14+ 26⋅ 13 7⋅14 + 1 3⋅13 267 ----------------= --------------= ----. 40 ⋅40 2 0⋅40 800

 
Odpowiedź: 267 800

Wersja PDF