Zadanie nr 9778331
Liczby ze zbioru 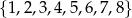 ustawiamy w przypadkowej kolejności (bez powtórzeń) tworząc liczbę ośmiocyfrową. Jakie jest prawdopodobieństwo otrzymania liczby, w której jednocześnie:
ustawiamy w przypadkowej kolejności (bez powtórzeń) tworząc liczbę ośmiocyfrową. Jakie jest prawdopodobieństwo otrzymania liczby, w której jednocześnie:
– cyfra 1 stoi na lewo od cyfry 2,
– cyfra 3 stoi na lewo od cyfry 4,
– cyfra 5 stoi na lewo od cyfry 6,
– cyfra 7 stoi na lewo od cyfry 8?
Uwaga, w powyższych warunkach nie zakładamy, że odpowiednie cyfry stoją obok siebie, np. liczba 13275846 spełnia wszystkie powyższe warunki.
Rozwiązanie
Wszystkich permutacji danego zbioru jest
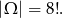
Sposób I
Jak policzyć zdarzenia sprzyjające? – zauważmy, że każde zdarzenie sprzyjające jest jednoznacznie wyznaczone przez wskazanie dwóch miejsc, na których będą cyfry 1 i 2 (nie ma wątpliwości jak umieścić te cyfry na tych dwóch miejscach: 1 na lewo, 2 na prawo), dwóch miejsc, na których będą 3 i 4, oraz dwóch miejsc, na których będą 5 i 6 – w takiej sytuacji cyfry 7 i 8 umieszczamy na dwóch pozostałych miejscach bez żadnego wyboru. Jest więc
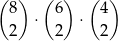
zdarzeń sprzyjających (wybieramy dwa miejsca dla 1 i 2, potem dwa miejsca dla 3 i 4, a na koniec dwa miejsca dla 5 i 6). Obliczmy wartość tego wyrażenia.
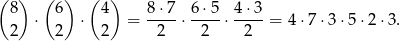
Prawdopodobieństwo jest więc równe
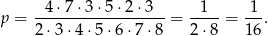
Sposób II
Zauważmy, że wśród zdarzeń elementarnych jest dokładnie tyle samo liczb, w których 1 jest na lewo od 2, jak tych, w których 1 jest na prawo od 2. Tak jest, bo każdej liczbie z 1 na lewo od 2 odpowiada dokładnie jedna liczba z 1 na prawo od 2 – wystarczy zamienić 1 i 2 miejscami. Jest więc
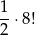
liczb z 1 na lewo od 2.
Analogicznie, wśród liczb z 1 na lewo od 2, dokładnie połowa liczb to liczby z 3 na lewo od 4 (tak jak poprzednio: każdej takiej liczbie odpowiada dokładnie jedna z 4 na lewo od 3). Jest więc
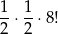
liczb spełniających pierwsze dwa warunki.
Dokładnie z tego samego powodu jest
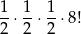
liczb spełniających pierwsze trzy warunki, oraz
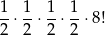
liczb, które spełniają wszystkie cztery warunki. Prawdopodobieństwo jest więc równe
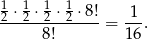
Sposób III
W skrócie: podzielimy wszystkie liczby ośmiocyfrowe o różnych cyfrach na 16 równolicznych zbiorów, przy czym interesujące nas liczby będą stanowiły jeden z tych zbiorów. To będzie oznaczać, że szukane prawdopodobieństwo wynosi 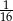 .
.
Każdej liczbie ośmiocyfrowej o różnych cyfrach przyporządkowujemy czteroelementowy ciąg zer i jedynek według następującej reguły: jeżeli liczba spełnia pierwszy z warunków zadania to na pierwszym miejscu dajemy 1, a jeżeli nie to dajemy 0; na drugim miejscu dajemy 1 jeżeli jest spełniony drugi warunek z treści zadania itd. Np. liczba, której przyporządkowano ciąg 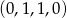 spełnia drugi i trzeci warunek, ale nie spełnia pierwszego i czwartego. Zauważmy teraz, że interesujące nas liczby to liczby, którym przyporządkowano ciąg
spełnia drugi i trzeci warunek, ale nie spełnia pierwszego i czwartego. Zauważmy teraz, że interesujące nas liczby to liczby, którym przyporządkowano ciąg 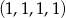 .
.
Wszystkich ciągów czteroelementowych o wyrazach 0 i 1 jest 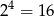 , więc podzieliliśmy w ten sposób wszystkie liczby ośmiocyfrowe na 16 zbiorów. Wystarczy teraz pokazać, że każde dwa z tych zbiorów mają tyle samo elementów.
, więc podzieliliśmy w ten sposób wszystkie liczby ośmiocyfrowe na 16 zbiorów. Wystarczy teraz pokazać, że każde dwa z tych zbiorów mają tyle samo elementów.
Zauważmy, że jeżeli we wszystkich liczbach odpowiadających ciągowi 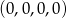 zamienimy miejscami cyfry 1 i 2 to otrzymamy wszystkie liczby odpowiadające ciągowi
zamienimy miejscami cyfry 1 i 2 to otrzymamy wszystkie liczby odpowiadające ciągowi 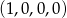 . Te dwa zbiory mają więc tyle samo elementów. Dokładnie w ten sam sposób uzasadniamy, że jeżeli dwa ciągi
. Te dwa zbiory mają więc tyle samo elementów. Dokładnie w ten sam sposób uzasadniamy, że jeżeli dwa ciągi 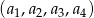 i
i 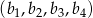 różnią się tylko w jednym miejscu to odpowiadające im zbiory liczb mają tyle samo elementów. Teraz wystarczy zauważyć, że zmieniając w jednym kroku tylko jedną liczbę można przejść od dowolnego ciągu do każdego innego. To oznacza, że każdy z 16 zbiorów ma tyle samo elementów, więc liczby odpowiadające ciągowi
różnią się tylko w jednym miejscu to odpowiadające im zbiory liczb mają tyle samo elementów. Teraz wystarczy zauważyć, że zmieniając w jednym kroku tylko jedną liczbę można przejść od dowolnego ciągu do każdego innego. To oznacza, że każdy z 16 zbiorów ma tyle samo elementów, więc liczby odpowiadające ciągowi 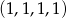 stanowią
stanowią 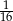 ogółu wszystkich liczb ośmiocyfrowych o różnych cyfrach.
ogółu wszystkich liczb ośmiocyfrowych o różnych cyfrach.

