Zadanie nr 9812182
Każdej karcie bankomatowej jest przypisany numer identyfikacyjny zwany kodem PIN. Kod ten składa się z czterech cyfr (cyfry mogą się powtarzać, ale kodem PIN nie może być 0000). Oblicz prawdopodobieństwo, że w losowo utworzonym kodzie PIN żadna cyfra się nie powtórzy. Wynik podaj w postaci ułamka nieskracalnego.
Rozwiązanie
Najpierw policzmy ile jest wszystkich możliwych numerów PIN. Każdą z cyfr można wybrać na 10 sposobów, czyli wszystkich możliwości wyboru 4 cyfr jest jest 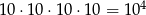 . Jeszcze trzeba odjąć 1 PIN odpowiadający 0000. W sumie mamy zatem
. Jeszcze trzeba odjąć 1 PIN odpowiadający 0000. W sumie mamy zatem 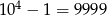 możliwych pinów.
możliwych pinów.
A ile jest tych z różnymi cyframi? Pierwszą cyfrę możemy wybrać dowolnie, czyli mamy 10 możliwości. Dla drugiej mamy już tylko 9 możliwości (bo nie możemy wziąć tej, którą wybraliśmy na pierwszym miejscu), dla trzeciej 8, a dla czwartej 7. Czyli razem jest 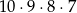 możliwości. Szukane prawdopodobieństwo wynosi zatem
możliwości. Szukane prawdopodobieństwo wynosi zatem
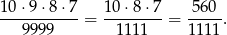
Liczba 1111 oczywiście nie jest podzielna przez ani przez 2 ani przez 5. Można też sprawdzić, że nie dzieli się przez 7. Oznacza to, że otrzymany ułamek jest nieskracalny.
Odpowiedź: