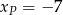/Szkoła średnia/Geometria/Geometria analityczna/Równanie prostej/Prosta przez dwa punkty

Zadanie nr 6997859

W układzie współrzędnych są dane punkty 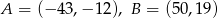A = (− 43,− 12), B = (50,1 9) . Prosta 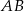AB przecina oś 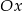Ox w punkcie 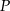P . Oblicz pierwszą współrzędną punktu P .

Wersja PDF

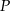Rozwiązanie

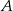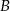Piszemy równanie prostej przechodzącej przez punkty A i B . Szukamy prostej w postaci 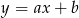y = ax + b i podstawiamy współrzędne danych punktów.

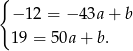
{ −1 2 = − 43a + b 19 = 50a + b.

Odejmujemy od drugiego równania pierwsze (żeby skrócić 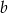b ) i mamy

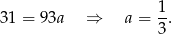
1 31 = 93a ⇒ a = -. 3

Mamy stąd 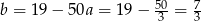b = 19 − 50a = 19 − 50 = 7 3 3 i prosta 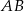AB ma równanie 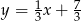1 7 y = 3x + 3 . Pozostało teraz wyznaczyć pierwszą współrzędną punktu wspólnego tej prostej z osią Ox .

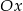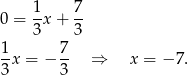
0 = 1x + 7- 3 3 1- 7- 3 x = − 3 ⇒ x = − 7.

 
Odpowiedź: xP = − 7

Wersja PDF