/Szkoła średnia/Geometria/Geometria analityczna/Równanie prostej/Z parametrem

Zadanie nr 2906859

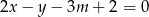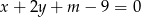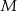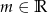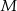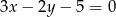Proste o równaniach: 2x − y − 3m + 2 = 0 i x + 2y + m − 9 = 0 przecinają się w punkcie M . Dla jakich wartości m ∈ R punkt M należy do prostej o równaniu 3x − 2y − 5 = 0 .

Wersja PDF

Rozwiązanie

Wyznaczmy punkt przecięcia się podanych dwóch prostych. W tym celu wstawiamy do pierwszego równania 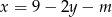x = 9− 2y− m wyliczony z drugiego równania.

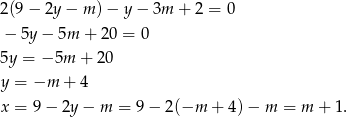
2(9 − 2y − m ) − y − 3m + 2 = 0 − 5y − 5m + 20 = 0 5y = − 5m + 2 0 y = −m + 4 x = 9− 2y− m = 9− 2(−m + 4 )− m = m + 1.

Pozostało sprawdzić, kiedy ten punkt leży na prostej 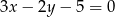3x − 2y − 5 = 0 (wstawiamy jego współrzędne do równania tej prostej).

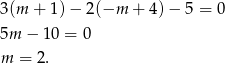
3(m + 1 )− 2(−m + 4) − 5 = 0 5m − 1 0 = 0 m = 2.

 
Odpowiedź: m = 2

Wersja PDF