/Szkoła średnia/Geometria/Geometria analityczna/Równanie prostej/Z parametrem

Zadanie nr 6782377

Dodaj do ulubionych
Dodaj do rozwiązanych

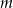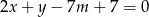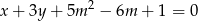Wyznacz te wartości parametru m , dla których punkt przecięcia się prostych o równaniach 2x + y − 7m + 7 = 0 i x + 3y + 5m 2 − 6m + 1 = 0 należy do 3 ćwiartki układu współrzędnych.

Rozwiązanie

Musimy wyznaczyć punkt przecięcia podanych prostych i sprawdzić kiedy ma on obie współrzędne ujemne. Odejmijmy od pierwszego z równań drugie pomnożone przez 2 (żeby skrócić x ).

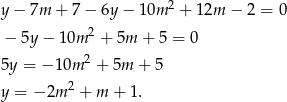
y − 7m + 7 − 6y − 10m 2 + 12m − 2 = 0 2 − 5y − 10m + 5m + 5 = 0 5y = − 10m 2 + 5m + 5 2 y = − 2m + m + 1.

Z drugiego równania mamy

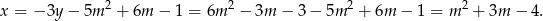
x = − 3y − 5m 2 + 6m − 1 = 6m 2 − 3m − 3 − 5m 2 + 6m − 1 = m 2 + 3m − 4 .

Mamy do rozwiązania nierówności

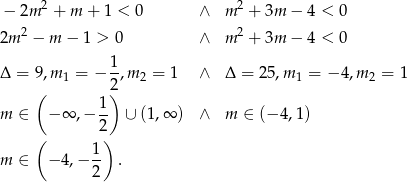
− 2m 2 + m + 1 < 0 ∧ m 2 + 3m − 4 < 0 2m 2 − m − 1 > 0 ∧ m 2 + 3m − 4 < 0 1 Δ = 9,m 1 = − -,m 2 = 1 ∧ Δ = 25,m 1 = − 4,m 2 = 1 ( 2) 1- m ∈ −∞ ,− 2 ∪ (1,∞ ) ∧ m ∈ (− 4 ,1 ) ( ) m ∈ −4 ,− 1- . 2

 
Odpowiedź: ( 1 ) m ∈ − 4,− 2

Wersja PDF