/Szkoła średnia/Geometria/Geometria analityczna/Równanie prostej/Z parametrem

Zadanie nr 8222592

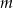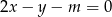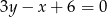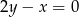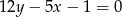Dla jakich wartości parametru m punkt przecięcia się prostych 2x − y − m = 0 i 3y − x + 6 = 0 należy do prostej 2y − x = 0 . Podaj współrzędne tego punktu i oblicz jego odległość od prostej 12y − 5x − 1 = 0 .

Wersja PDF

Rozwiązanie

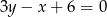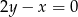Sprawdźmy w jakim punkcie przecinają się proste 3y − x + 6 = 0 i 2y − x = 0 . Podstawiamy za x do pierwszego równania z drugiego równania i mamy

3y − 2y + 6 = 0 ⇒ y = − 6.

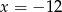Stąd x = − 12 . Aby był spełniony podany w zadaniu warunek, prosta 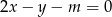2x − y − m = 0 musi przechodzić przez punkt 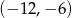(− 12,− 6) . Stąd

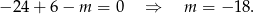
− 2 4+ 6 − m = 0 ⇒ m = − 18.

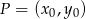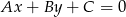Korzystamy teraz ze wzoru na odległość punktu P = (x 0,y 0) od prostej Ax + By + C = 0 :

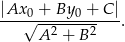
|Ax-0√-+-By-0 +-C|. A 2 + B 2

W naszej sytuacji mamy

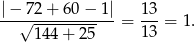
|−-72-+-6-0−-1-| 13- √ 14-4+--25 = 13 = 1.

 
Odpowiedź: 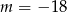m = − 18 , punkt: 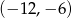(− 12,− 6) , odległość: 1

Wersja PDF