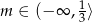/Szkoła średnia/Geometria/Geometria analityczna/Równanie prostej/Z parametrem

Zadanie nr 9186387

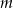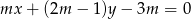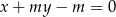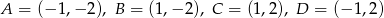Zbadaj dla jakich wartości parametru m punkt przecięcia się prostych mx + (2m − 1)y − 3m = 0 i x + my − m = 0 należy do prostokąta o wierzchołkach A = (−1 ,−2 ), B = (1,− 2), C = (1,2), D = (− 1,2) ?

Wersja PDF

Rozwiązanie

Po pierwsze, należy rozszyfrować co to znaczy, że jakiś punkt 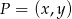P = (x,y ) należy do podanego prostokąta.

PIC

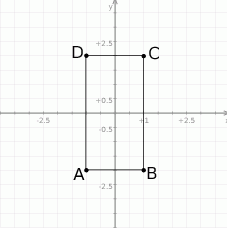
Jeżeli go sobie naszkicujemy w układzie współrzędnych, to widać, że warunek ten sprowadza się do dwóch podwójnych nierówności

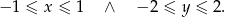
− 1 ≤ x ≤ 1 ∧ − 2 ≤ y ≤ 2.

Musimy zatem znaleźć punkt 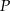P wspólny podanych prostych i sprawdzić kiedy spełnia on powyższe nierówności. Aby wyznaczyć 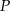P musimy rozwiązać układ równań

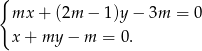
{ mx + (2m − 1 )y− 3m = 0 x + my − m = 0.

Odejmujemy od pierwszego równania drugie pomnożone przez 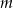m (żeby skrócić x ).

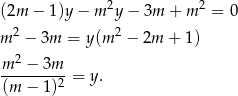
(2m − 1 )y− m2y − 3m + m 2 = 0 m 2 − 3m = y (m2 − 2m + 1) 2 m--−--3m-= y. (m − 1)2

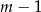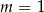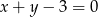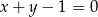Po drodze dzieliliśmy przez m − 1 , więc sprawdźmy jeszcze co się dzieje dla m = 1 . Mamy wtedy proste x+ y− 3 = 0 i x + y − 1 = 0 , które nie mają punktów wspólnych.

Wracamy do wyliczenia 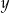y . Z drugiego równania układu mamy

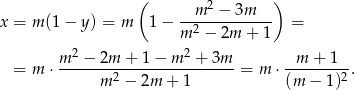
( 2 ) x = m (1 − y) = m 1 − --m---−-3m--- = m 2 − 2m + 1 2 2 = m ⋅ m--−-2m--+-1-−-m--+--3m- = m ⋅ -m-+--1--. m 2 − 2m + 1 (m − 1 )2

Zajmijmy się teraz nierównością 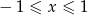− 1 ≤ x ≤ 1 . Ponieważ 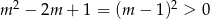m 2 − 2m + 1 = (m − 1)2 > 0 mamy

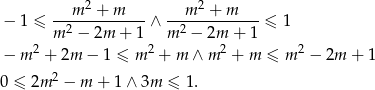
--m-2 +-m---- ---m2-+-m---- − 1 ≤ m2 − 2m + 1 ∧ m 2 − 2m + 1 ≤ 1 2 2 2 2 − m + 2m − 1 ≤ m + m ∧ m + m ≤ m − 2m + 1 0 ≤ 2m2 − m + 1∧ 3m ≤ 1.

Nierówność kwadratowa jest zawsze spełniona (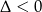Δ < 0 ) więc pozostaje 1 m ≤ 3 .

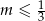Pora na nierówność 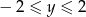− 2 ≤ y ≤ 2 .

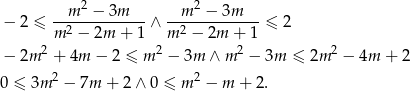
2 2 − 2 ≤ --m--−--3m---∧ --m--−-3m----≤ 2 m 2 − 2m + 1 m 2 − 2m + 1 − 2m 2 + 4m − 2 ≤ m2 − 3m ∧ m2 − 3m ≤ 2m 2 − 4m + 2 0 ≤ 3m 2 − 7m + 2∧ 0 ≤ m 2 − m + 2.

Druga nierównosć jest zawsze spełniona (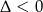Δ < 0 ), zajmijmy się więc pierwszą.

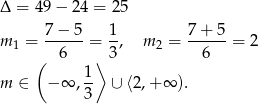
Δ = 49 − 24 = 25 m = 7-−-5-= 1-, m = 7-+-5-= 2 1 6 3 2 6 ( 1⟩ m ∈ − ∞ ,-- ∪ ⟨2,+ ∞ ). 3

W połączeniu z wcześniej uzyskaną nierównością daje to nam 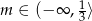1 m ∈ (− ∞ ,3⟩ .  
Odpowiedź: m ∈ (− ∞ , 1⟩ 3

Wersja PDF