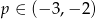/Szkoła średnia/Geometria/Geometria analityczna/Równanie prostej/Z parametrem

Zadanie nr 9510753

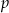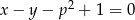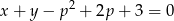Dla jakich wartości parametru p proste 2 x − y − p + 1 = 0 i x + y − p 2 + 2p + 3 = 0 przecinają się w punkcie należącym do wnętrza prostokąta o wierzchołkach A = (4,− 1) , B = (10,− 1) , C = (10,2 ) , D = (4,2 ) ?

Wersja PDF

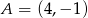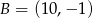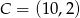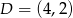Rozwiązanie

Po pierwsze należy rozszyfrować co to znaczy, że jakiś punkt 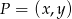P = (x,y) należy do podanego prostokąta.

PIC

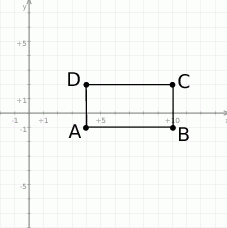
Jeżeli go sobie naszkicujemy w układzie współrzędnych, to widać, że warunek ten sprowadza się do dwóch podwójnych nierówności

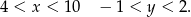
4 < x < 10 − 1 < y < 2 .

Musimy zatem znaleźć punkt 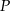P wspólny podanych prostych i sprawdzić kiedy spełnia on powyższe nierówności. Aby wyznaczyć 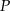P dodajemy równania prostych stronami (żeby skrócić y ).

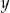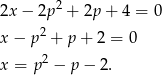
2 2x − 2p + 2p + 4 = 0 x − p2 + p + 2 = 0 2 x = p − p − 2.

Z pierwszego równania mamy

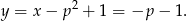
y = x− p2 + 1 = −p − 1.

Pozostało rozwiązać nierówności. Łatwiej jest z 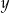y -kiem, więc od niego zacznijmy.

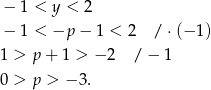
− 1 < y < 2 − 1 < −p − 1 < 2 / ⋅(− 1) 1 > p + 1 > − 2 /− 1 0 > p > − 3.

Teraz pora na x -a.

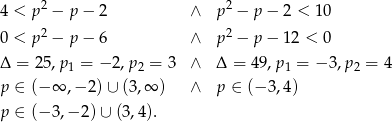
2 2 4 < p − p− 2 ∧ p − p − 2 < 10 0 < p 2 − p− 6 ∧ p2 − p − 12 < 0 Δ = 25,p 1 = − 2,p2 = 3 ∧ Δ = 4 9,p1 = − 3,p2 = 4 p ∈ (− ∞ ,− 2) ∪ (3,∞ ) ∧ p ∈ (− 3,4) p ∈ (− 3,− 2) ∪ (3,4).

W połączeniu z wcześniej uzyskaną nierównością 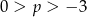0 > p > − 3 , mamy p ∈ (− 3 ,− 2 ) .  
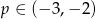Odpowiedź: p ∈ (− 3,− 2)

Wersja PDF