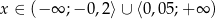Zadanie nr 1048358
Rozwiąż nierówność: 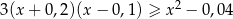 .
.
Rozwiązanie
Sposób I
Liczymy
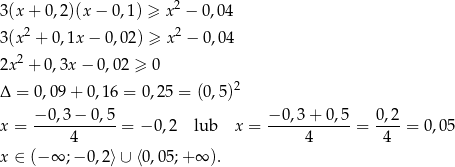
Sposób II
Widać, że po obu stronach nierówności powtarza się czynnik 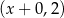 .
.
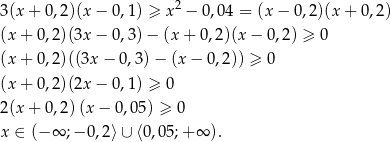
Odpowiedź: 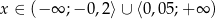
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Rozwiąż nierówność: 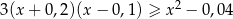 .
.
Sposób I
Liczymy
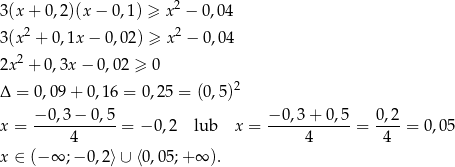
Sposób II
Widać, że po obu stronach nierówności powtarza się czynnik 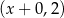 .
.
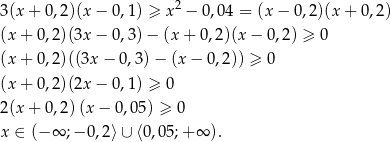
Odpowiedź: