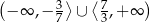/Szkoła średnia/Nierówności/Kwadratowe/Rozwiąż nierówność

Zadanie nr 1273538

Rozwiąż nierówność 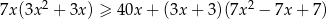2 2 7x (3x + 3x) ≥ 40x + (3x+ 3)(7x − 7x + 7) .

Wersja PDF

Rozwiązanie

Sposób I

Przekształcamy daną nierówność.

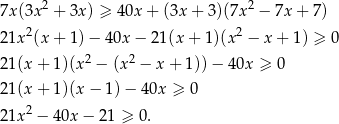
2 2 7x(3x + 3x ) ≥ 40x + (3x + 3)(7x − 7x + 7) 21x2(x + 1) − 40x − 2 1(x+ 1)(x2 − x + 1) ≥ 0 2 2 21(x + 1)(x − (x − x + 1)) − 40x ≥ 0 21(x + 1)(x − 1) − 40x ≥ 0 2 21x − 40x − 21 ≥ 0.

Pozostało rozwiązać otrzymaną nierówność kwadratową.

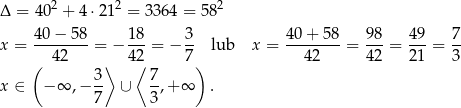
2 2 2 Δ = 40 + 4 ⋅21 = 336 4 = 58 40 − 58 18 3 40+ 58 98 4 9 7 x = --------= − ---= − -- lub x = --------= ---= --- = -- ( 4 2 ⟩ 42⟨ 7) 42 42 2 1 3 x ∈ − ∞ ,− 3- ∪ 7,+ ∞ . 7 3

Sposób II

Przekształcamy daną nierówność.

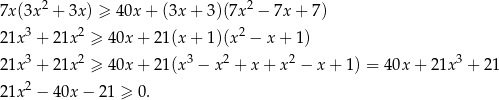
7x(3x2 + 3x) ≥ 40x + (3x + 3)(7x 2 − 7x + 7) 21x3 + 21x2 ≥ 4 0x+ 21(x + 1)(x2 − x + 1) 3 2 3 2 2 3 21x + 21x ≥ 4 0x+ 21(x − x + x + x − x + 1) = 4 0x+ 21x + 21 21x2 − 40x − 21 ≥ 0.

Otrzymaną nierówność kwadratową rozwiązujemy tak samo jak w poprzednim sposobie.  
Odpowiedź: ( ⟩ ⟨ ) − ∞ ,− 3 ∪ 7,+ ∞ 7 3

Wersja PDF