/Szkoła średnia/Nierówności/Kwadratowe/Rozwiąż nierówność

Zadanie nr 5103782

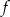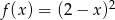Funkcja kwadratowa f jest określona wzorem 2 f(x) = (2 − x) .

  • Wyznacz najmniejszą i największą wartość funkcji 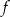f w przedziale ⟨0,5⟩ .
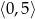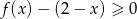  • Rozwiąż nierówność f(x) − (2 − x) ≥ 0 .
Wersja PDF

Rozwiązanie

Ponieważ 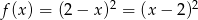2 2 f(x) = (2 − x ) = (x− 2) , to wykresem tej funkcji jest parabola z ramionami skierowanymi do góry, styczna do osi 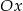Ox w punkcie 2 .

PIC

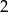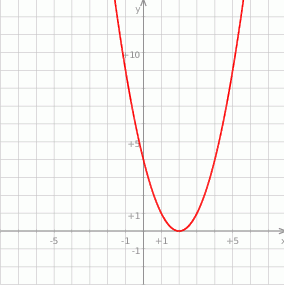
  • Ponieważ wierzchołek paraboli jest w danym przedziale, to właśnie w nim jest najmniejsza wartość f(2 ) = 0 .

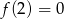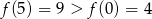    Ze względu na kształt wykresu, największa wartość jest w jednym z końców przedziału. Łatwo sprawdzić, że f(5) = 9 > f(0) = 4 .  
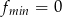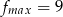
    Odpowiedź: f = 0 min , f = 9 max

  • Przekształćmy podaną nierówność
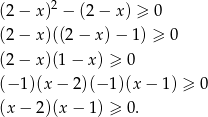
    (2 − x)2 − (2 − x) ≥ 0 (2 − x)((2 − x )− 1) ≥ 0 (2 − x)(1 − x ) ≥ 0 (− 1)(x − 2)(− 1)(x − 1 ) ≥ 0 (x − 2)(x − 1 ) ≥ 0.

    Nierówność, którą otrzymaliśmy to najwyklejsza nierówność kwadratowa, jej rozwiązaniem jest zbiór 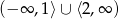(− ∞ ,1⟩∪ ⟨2,∞ ) (oba czynniki mają być nieujemne lub oba niedodatnie).  
    Odpowiedź: (− ∞ ,1⟩∪ ⟨2,∞ )

Wersja PDF