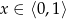Zadanie nr 5296444
Dane są funkcje 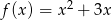 i
i 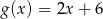 . Rozwiąż nierówność
. Rozwiąż nierówność 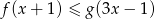 .
.
Rozwiązanie
Liczymy
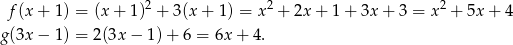
Mamy więc nierówność
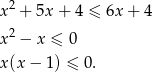
Jest to zwykła nierówność kwadratowa, jej rozwiązaniem jest zbiór 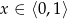 .
.
Odpowiedź: 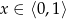
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dane są funkcje 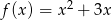 i
i 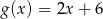 . Rozwiąż nierówność
. Rozwiąż nierówność 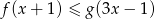 .
.
Liczymy
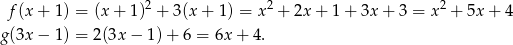
Mamy więc nierówność
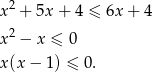
Jest to zwykła nierówność kwadratowa, jej rozwiązaniem jest zbiór 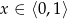 .
.
Odpowiedź: