Zadanie nr 7019024

Rozwiąż nierówność 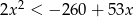2 2x < − 260 + 53x . Podaj wszystkie liczby całkowite, które spełniają tę nierówność.

Rozwiązanie

Zapiszmy nierówność w postaci

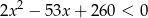
2 2x − 53x + 26 0 < 0

i liczymy standardowo, z 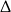-y.

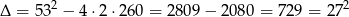
2 2 Δ = 53 − 4⋅ 2⋅26 0 = 2809 − 20 80 = 729 = 27

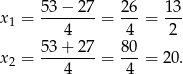
53 − 27 26 13 x 1 = --------= ---= --- 4 4 2 x 2 = 53-+-27-= 80-= 20. 4 4

Możemy teraz naszkicować wykres tej funkcji

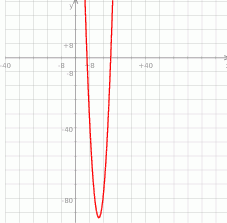
Widać teraz, że rozwiązaniem nierówności jest przedział

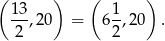
( ) ( ) 1-3,20 = 61-,20 . 2 2

Jeżeli chodzi liczby całkowite w tym przedziale, to są to wszystkie liczby całkowite z przedziału 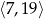⟨7,19⟩ , czyli

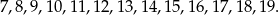
7,8,9,10,11 ,12,13,14,15 ,16,17,18,19 .

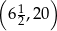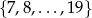Odpowiedź: ( ) 1 62,2 0 , { 7,8,...,19} .

Nie rozumiesz fragmentu rozwiązania?
W rozwiązaniu jest błąd lub literówka?
Masz inny pomysł na rozwiązanie tego zadania?
Napisz nam o tym!

Dodaj komentarz