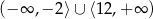/Szkoła średnia/Nierówności/Kwadratowe/Rozwiąż nierówność

Zadanie nr 8598047

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż nierówność: 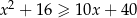2 x + 16 ≥ 10x + 40 .

Rozwiązanie

Musimy rozwiązać nierówność

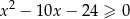
2 x − 10x − 2 4 ≥ 0

Znajdujemy najpierw miejsca zerowe trójmianu 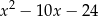2 x − 10x − 24

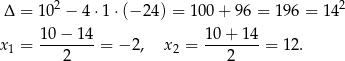
2 2 Δ = 1 0 − 4 ⋅1 ⋅(− 24) = 10 0+ 96 = 196 = 14 10−--14- 10-+-1-4 x1 = 2 = − 2 , x2 = 2 = 12.

Ponieważ współczynnik przy 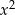x 2 jest dodatni, wykres tego trójmianu jest parabolą o ramionach skierowanych do góry.

PIC

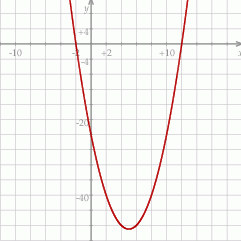
Otrzymujemy stąd rozwiązanie nierówności: 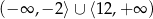(−∞ ,− 2⟩ ∪ ⟨12,+ ∞ ) .  
Odpowiedź: (− ∞ ,− 2⟩ ∪ ⟨12,+ ∞ )

Wersja PDF