Zadanie nr 9184364
Dane są funkcje 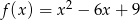 i
i 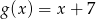 .
.
- Znajdź te argumenty, dla których zarówno funkcja
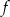 , jak i funkcja
, jak i funkcja 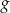 przyjmują wartości dodatnie.
przyjmują wartości dodatnie. - Uzasadnij, że dla każdej liczby całkowitej
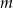 liczba
liczba 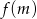 jest kwadratem liczby całkowitej. Kwadratem jakiej liczby naturalnej jest
jest kwadratem liczby całkowitej. Kwadratem jakiej liczby naturalnej jest 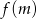 , jeżeli
, jeżeli 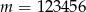 ?
?
Rozwiązanie
- Zauważmy, że
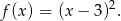
Zatem
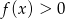 dla
dla 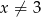 . Ponadto
. Ponadto 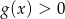 dla
dla 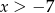 . Zatem
. Zatem 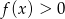 i
i 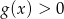 dla
dla 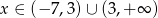 .
.
Odpowiedź: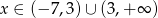
- Jak zauważyliśmy wcześniej,
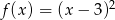 . Zatem dla
. Zatem dla 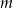 całkowitych,
całkowitych, 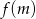 jest kwadratem liczby całkowitej.
jest kwadratem liczby całkowitej. Jeżeli
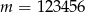 , to
, to 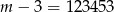 i
i 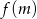 jest kwadratem tej liczby.
jest kwadratem tej liczby.
Odpowiedź: 123453

