Zadanie nr 1164803
Niech  będzie liczbą naturalną. Ze zbioru liczb
będzie liczbą naturalną. Ze zbioru liczb 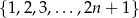 losujemy dwie liczby (mogą być równe). Oblicz prawdopodobieństwo, że suma wylosowanych liczb będzie większa od
losujemy dwie liczby (mogą być równe). Oblicz prawdopodobieństwo, że suma wylosowanych liczb będzie większa od 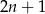 .
.
Rozwiązanie
Jeżeli za zdarzenia elementarne przyjmiemy uporządkowane pary 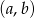 wylosowanych liczb, to
wylosowanych liczb, to
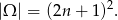
Policzmy teraz ilość zdarzeń sprzyjających Jeżeli pierwszą z wylosowanych liczb jest:
1 – to na drugą mamy 1 możliwość: 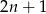 ,
,
2 – to na drugą mamy 2 możliwości: 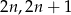 ,
,
3 – to na drugą mamy 3 możliwości: 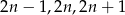 ,
,
…,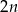 – to na drugą mamy
– to na drugą mamy 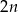 możliwości:
możliwości: 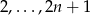 ,
,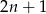 – to na drugą mamy
– to na drugą mamy 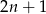 możliwości:
możliwości: 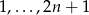 .
.
Wszystkich zdarzeń sprzyjających jest zatem
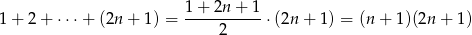
(skorzystaliśmy ze wzoru na sumę kolejnych wyrazów ciągu arytmetycznego). Zatem
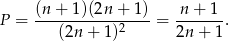
Odpowiedź: