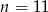Zadanie nr 1220479
W zbiorze 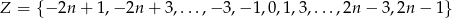 , gdzie
, gdzie 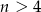 jest liczbą naturalną, zmieniono znaki na przeciwne trzem losowo wybranym liczbom. Wiadomo, że prawdopodobieństwo tego, że suma wszystkich liczb w zbiorze nie uległa zmianie wynosi
jest liczbą naturalną, zmieniono znaki na przeciwne trzem losowo wybranym liczbom. Wiadomo, że prawdopodobieństwo tego, że suma wszystkich liczb w zbiorze nie uległa zmianie wynosi 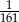 . Wyznacz
. Wyznacz  .
.
Rozwiązanie
Policzmy ile jest liczb w danym zbiorze. Ponieważ
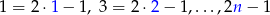
tych liczb jest  . W całym zbiorze jest więc
. W całym zbiorze jest więc 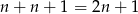 liczb. Zatem możliwości wybrania trzech z nich jest
liczb. Zatem możliwości wybrania trzech z nich jest
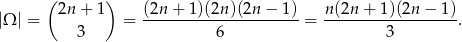
Jeżeli 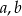 i
i  są liczbami, przy których zmieniono znaki, to suma wszystkich liczb się nie zmieni tylko wtedy gdy
są liczbami, przy których zmieniono znaki, to suma wszystkich liczb się nie zmieni tylko wtedy gdy 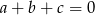 (bo
(bo 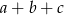 jest kawałkiem tej sumy i zmienia znak na przeciwny). Jest jednak mały problem, w danym zbiorze jest tylko jedna liczba parzysta, a w równości
jest kawałkiem tej sumy i zmienia znak na przeciwny). Jest jednak mały problem, w danym zbiorze jest tylko jedna liczba parzysta, a w równości 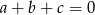 nie mogą wszystkie trzy liczby być nieparzyste. Zatem jedna z tych liczb, powiedzmy
nie mogą wszystkie trzy liczby być nieparzyste. Zatem jedna z tych liczb, powiedzmy  jest równa 0. Mamy w takim razie równość
jest równa 0. Mamy w takim razie równość 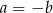 . Ile jest takich par? – to łatwe, tyle ile jest liczb dodatnich w danym zbiorze, czyli
. Ile jest takich par? – to łatwe, tyle ile jest liczb dodatnich w danym zbiorze, czyli  . Mamy zatem równanie
. Mamy zatem równanie
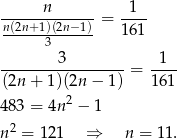
Odpowiedź: