/Szkoła średnia/Prawdopodobieństwo

Zadanie nr 1324389

Dodaj do ulubionych
Dodaj do rozwiązanych

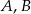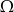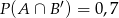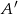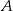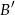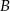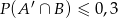Zdarzenia losowe A ,B są zawarte w Ω oraz ′ P (A ∩ B ) = 0,7 ( ′ A oznacza zdarzenie przeciwne do zdarzenia A , B′ oznacza zdarzenie przeciwne do zdarzenia B ). Wykaż, że P (A ′ ∩ B) ≤ 0 ,3 .

Rozwiązanie

Rysujemy diagram Venna

PIC

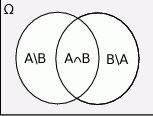
Sposób I

Z diagramu widać, że

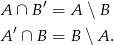
′ A ∩ B = A ∖ B A ′ ∩ B = B ∖A .

W szczególności zdarzenia te są rozłączne, czyli

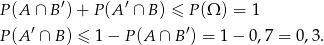
P(A ∩ B′)+ P(A ′ ∩ B ) ≤ P(Ω ) = 1 ′ ′ P(A ∩ B ) ≤ 1− P(A ∩ B ) = 1 − 0,7 = 0,3 .

Sposób II

Z diagramu widać, że

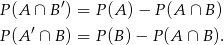
P(A ∩ B ′) = P(A )− P(A ∩ B) P(A ′ ∩ B ) = P(B )− P (A ∩ B ).

Wiemy zatem że

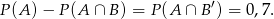
′ P (A )− P (A ∩ B ) = P(A ∩ B ) = 0,7.

Wiemy ponadto, że

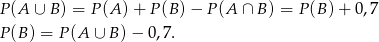
P (A ∪ B) = P(A )+ P(B )− P (A ∩ B ) = P(B )+ 0,7 P (B) = P (A ∪ B )− 0,7 .

Musimy zatem wykazać nierówność

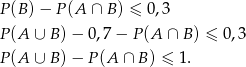
P (B)− P(A ∩ B) ≤ 0,3 P (A ∪ B) − 0,7 − P (A ∩ B ) ≤ 0,3 P (A ∪ B) − P (A ∩ B) ≤ 1.

A ta nierówność jest oczywista (bo 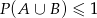P(A ∪ B ) ≤ 1 ).

Wersja PDF