/Szkoła średnia/Prawdopodobieństwo

Zadanie nr 1340789

Dodaj do ulubionych
Dodaj do rozwiązanych

W grze liczbowej Express Lotek losowanych jest pięć spośród liczb 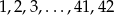1,2,3 ,...,41,42 . Gracz zawarł jeden zakład na najbliższe losowanie (czyli wytypował w kolekturze Totalizatora Sportowego pięć liczb spośród czterdziestu dwóch). Oblicz ile razy prawdopodobieństwo trafienia ’trójki’ (czyli wytypowania dokładnie 3 liczb spośród tych, które będą wylosowane) jest większe niż prawdopodobieństwo trafienia

  • piątki;
  • czwórki.

Rozwiązanie

Jeżeli za zdarzenia elementarne przyjmiemy zbiory (nieuporządkowane) 5 wylosowanych liczb, to mamy

( ) |Ω | = 42 . 5

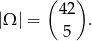
Tak naprawdę ta wartość nie będzie nam potrzebna, bo nie mamy liczyć prawdopodobieństw, ale tylko je dzielić, więc wystrczy dzielić liczby zdarzeń sprzyjających.

Powiedzmy, że jest ustalonych 5 wylosowanych liczb. Ustalmy ile jest skreśleń 5 liczb, w których dokładnie 3 liczby są takie jak w wylosowanej piątce. Pasującą trójkę możemy dobrać na

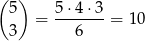
( ) 5 = 5⋅-4⋅3-= 10 3 6

sposobów. Do tych trzech liczb trzeba dobrać jeszcze dwie z przegrywających. Można to zrobić na

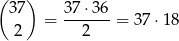
( ) 37 37⋅ 36 = -------= 37 ⋅18 2 2

sposobów. Razem mamy więc

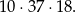
10⋅ 37⋅1 8.

zdarzeń sprzyjających.

  • Jest tylko jedno zdarzenie sprzyjające, więc szukany iloraz wynosi
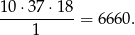
    1-0⋅37-⋅18-= 6660. 1

     
    Odpowiedź: 6660

  • Liczymy tak jak przy trójce. 4 pasujące liczby możemy wybrać ze szczęśliwej piątki na 5 sposobów, do nich trzeba dobrać jedną z pozostałych 37, czyli jest
    37 ⋅5

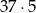
    zdarzeń sprzyjających. Szukany iloraz wynosi

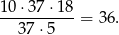
    10⋅3-7⋅18-= 36. 37 ⋅5

     
    Odpowiedź: 36

Wersja PDF