/Szkoła średnia/Prawdopodobieństwo

Zadanie nr 1587219

Dodaj do ulubionych
Dodaj do rozwiązanych

Liczby ze zbioru 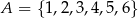A = {1,2,3,4,5,6 } ustawiamy w losowy sposób w sześcioelementowy ciąg, przy czym każda liczba ze zbioru 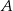A jest dokładnie jednym wyrazem tego ciągu. Oblicz prawdopodobieństwo tego, że iloczyn każdych dwóch sąsiednich wyrazów tego ciągu jest liczbą parzystą jeżeli wiadomo, że pierwszy wyraz tego ciągu jest liczbą nieparzystą.

Rozwiązanie

Rozwiązanie tego zadania jest dostępne tylko dla użytkowników z wykupionym abonamentem.
Zaloguj się Informacje o abonamencie
Nie chcesz się rejestrować ani opłacać abonamentu? Zapłać przelewem 7,90 zł lub telefonicznie 9,90 zł, a otrzymasz dwudziestominutowy dostęp do wszystkich materiałów dostępnych w portalu.