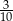Zadanie nr 1637028
Doświadczenie losowe polega na tym, że losujemy jednocześnie trzy liczby ze zbioru
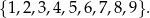
Oblicz prawdopodobieństwo warunkowe, że wśród wylosowanych liczb będzie liczba 3, pod warunkiem, że suma wylosowanych liczb będzie nieparzysta. Wynik przedstaw w postaci ułamka nieskracalnego.
Rozwiązanie
Niech 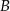 oznacza zdarzenie polegające na otrzymaniu trzech liczb, których suma jest nieparzysta, a
oznacza zdarzenie polegające na otrzymaniu trzech liczb, których suma jest nieparzysta, a 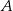 niech będzie zdarzeniem polegającym na wylosowaniu liczb, wśród których jest liczba 3. Musimy zatem obliczyć
niech będzie zdarzeniem polegającym na wylosowaniu liczb, wśród których jest liczba 3. Musimy zatem obliczyć
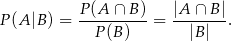
Zajmijmy się najpierw zdarzeniem 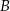 . Jeżeli suma wybranych liczb jest nieparzysta to albo wszystkie są nieparzyste, albo dokładnie jedna z nich jest nieparzysta. Zdarzeń pierwszego typu jest
. Jeżeli suma wybranych liczb jest nieparzysta to albo wszystkie są nieparzyste, albo dokładnie jedna z nich jest nieparzysta. Zdarzeń pierwszego typu jest
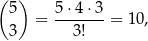
a zdarzeń drugiego typu jest
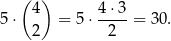
Mamy zatem
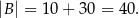
Zajmijmy się teraz zdarzeniem 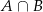 . Wystarczy się zastanowić na ile sposobów można wybrać ze zbioru
. Wystarczy się zastanowić na ile sposobów można wybrać ze zbioru
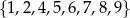
dwie liczby, których suma jest parzysta (bo wtedy łącznie z 3 dadzą sumę nieparzystą). Dwie liczby parzyste możemy wybrać na
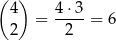
sposobów. Dokładnie tyle samo jest możliwości wybrania dwóch liczb nieparzystych, więc
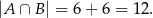
Interesujące nas prawdopodobieństwo jest więc równe
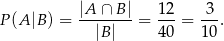
Odpowiedź: