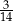Zadanie nr 1891670
Ze zbioru ośmiu kolejnych liczb naturalnych – od 1 do 8 – losujemy kolejno bez zwracania dwa razy po jednej liczbie. Niech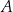 
oznacza zdarzenie polegające na tym, że suma wylosowanych liczb jest dzielnikiem liczby 12. Oblicz prawdopodobieństwo zdarzenia 
.
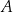Rozwiązanie
Dwie cyfry z podanego zbioru można wybrać na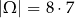 
sposobów. Zdarzenia sprzyjające to takie, gdzie suma wylosowanych liczb jest równa 1, 2, 3, 4, 6 lub 12. Wypiszmy wszystkie takie liczby
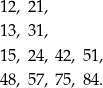
(Liczby: 11, 22, 33 i 66 nie spełniają warunku losowania bez zwracania.) Prawdopodobieństwo zdarzenia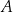 
jest więc równe
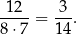
Odpowiedź: 
