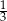/Szkoła średnia/Prawdopodobieństwo

Zadanie nr 2294963

Dodaj do ulubionych
Dodaj do rozwiązanych

Gracz rzuca dwukrotnie symetryczną sześcienną kostką do gry i oblicza wartość bezwzględną różnicy liczb wyrzuconych oczek. Oblicz prawdopodobieństwo zdarzenia 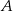A polegającego na tym, że obliczona wartość bezwzględna różnicy wyrzuconych oczek jest równa 3, 4 lub 5.

Rozwiązanie

Przyjmijmy, że zdarzenia elementarne to uporządkowane pary wylosowanych liczb. Zatem

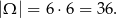
|Ω | = 6 ⋅6 = 36 .

Wypiszmy zdarzenia sprzyjające:

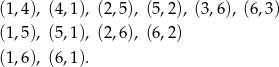
(1,4), (4,1), (2,5), (5,2), (3 ,6), (6,3) (1,5), (5,1), (2,6), (6,2) (1,6), (6,1).

Jak widać jest 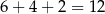6 + 4 + 2 = 12 zdarzeń sprzyjających i interesujące nas prawdopodobieństwo jest równe

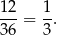
12-= 1. 36 3

 
Odpowiedź: 1 3

Wersja PDF