Zbiory i ich elementy Przypomnijmy, że zbiór składa się z elementów. Jeżeli  jest elementem zbioru
jest elementem zbioru 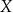 to piszemy
to piszemy
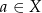
i czytamy „ należy do zbioru
należy do zbioru 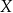 ”.
”.
Jeżeli  nie jest elementem zbioru
nie jest elementem zbioru 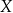 to piszemy
to piszemy
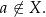
Jeżeli każdy element zbioru 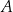 jest jednocześnie elementem zbioru
jest jednocześnie elementem zbioru 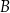 , to mówimy, że
, to mówimy, że 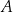 jest podzbiorem zbioru
jest podzbiorem zbioru 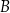 (lub, że
(lub, że 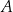 zawiera się w
zawiera się w 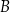 ) i piszemy
) i piszemy
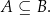
Mówimy, że dwa zbiory 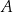 i
i 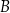 są równe jeżeli składają się dokładnie z tych samych elementów. Piszemy wtedy
są równe jeżeli składają się dokładnie z tych samych elementów. Piszemy wtedy
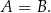
Jeżeli 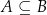 oraz
oraz 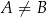 to mówimy, że
to mówimy, że 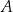 jest podzbiorem właściwym
jest podzbiorem właściwym 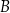 . Piszemy wtedy
. Piszemy wtedy
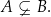
Zbiór, który nie ma żadnych elementów nazywamy zbiorem pustym i oznaczamy symbolem 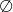 .
.
Zauważmy, że dla dowolnego zbioru 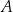 mamy
mamy 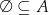 .
.
Różne sposoby definiowania zbiorów 1. Opis słowny. Tego typu definicje zbiorów stosujemy co rusz w naszym codziennym życiu, często nie zdając sobie nawet z tego sprawy.
Mówiąc „wszyscy uczniowie klasy IIa” mamy na myśli zbiór składający się z uczniów tej klasy.
Opis słowny pozwala nam definiować zbiory, których nawet nie jesteśmy w stanie sobie wyobrazić, np. „zbiór wszystkich atomów we wszechświecie”.
2. Rysunek. Schematyczne rysunki obrazujące zbiory jako „worki z elementami” są często bardzo wygodne, bo pozwalają łatwo ilustrować różne ich własności.
Lewy diagram przedstawia (symbolicznie) zbiór 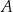 , który ma 6 elementów.
, który ma 6 elementów.
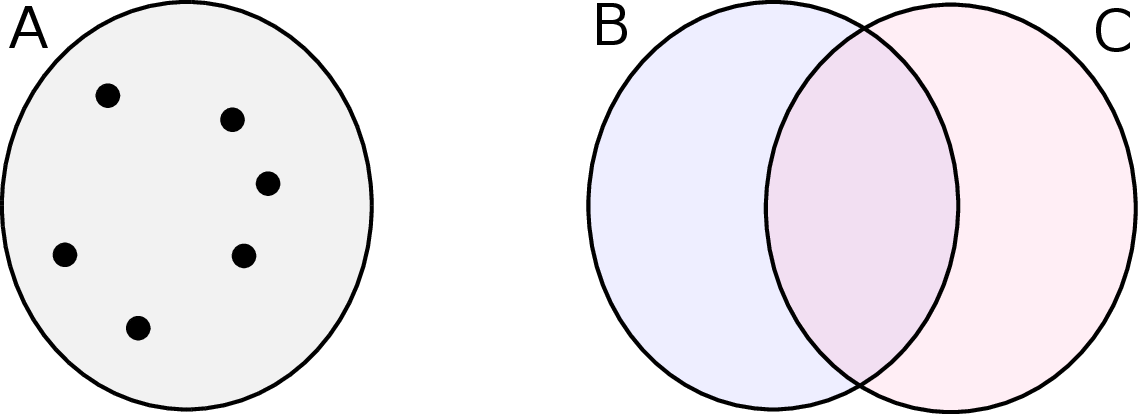
Zwróćmy uwagę, że sam diagram nic nam nie mówi o tym, jaka jest natura elementów zbioru 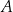 (czy to są liczby, jabłka, a może jeszcze coś innego). O tego typu diagramie mówimy, że jest abstrakcyjny, bo abstrahuje od (nie uwzględnia) natury zbioru
(czy to są liczby, jabłka, a może jeszcze coś innego). O tego typu diagramie mówimy, że jest abstrakcyjny, bo abstrahuje od (nie uwzględnia) natury zbioru 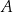 oraz jego elementów.
oraz jego elementów.
Często posuwamy się jeszcze dalej i rysujemy zbiory w ogóle nie zaznaczając ich elementów. Tak właśnie rozumiemy prawy diagram, który ilustruje możliwe relacje między elementami dwóch zbiorów 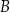 i
i 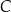 . Pomimo, że nie zaznaczyliśmy ani jednego elementu zbiorów
. Pomimo, że nie zaznaczyliśmy ani jednego elementu zbiorów 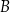 i
i 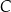 , wymowa diagramu powinna być jasna: jeżeli mamy dwa zbiory
, wymowa diagramu powinna być jasna: jeżeli mamy dwa zbiory 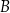 i
i 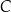 to mogą być elementy, które należą tylko do
to mogą być elementy, które należą tylko do 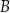 , elementy które należą tylko do
, elementy które należą tylko do 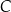 , oraz elementy, które należą do obu zbiorów naraz.
, oraz elementy, które należą do obu zbiorów naraz.
Poniższy diagram
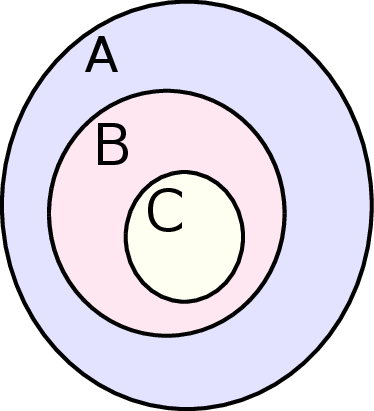
jest symboliczną ilustracją trzech zbiorów spełniających warunek
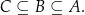
3. Wypisanie elementów. W przypadku zbiorów skończonych możemy wypisać wszystkie elementy zbioru. Robimy to umieszczając elementy zbioru w klamerkach: 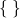 .
.
Zbiór zawierający 5 pierwszych liter alfabetu możemy zapisać w postaci
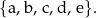
W przypadku większych zbiorów stosujemy czasem notację z wielokropkiem, licząc na to, że czytelnik domyśli się o jaki zbiór nam chodzi. Np. domyślamy się, że zapis
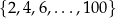
ma oznaczać zbiór parzystych liczb naturalnych nie większych niż 100.
Podobną konwencję stosuje się też czasem w przypadku zbiorów nieskończonych, np. domyślamy się, że zapis
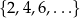
ma oznaczać zbiór liczb parzystych.
Zbiór zawiera tylko informację o tym, czy dany element do niego należy, czy nie. Nie zawiera natomiast informacji o kolejności elementów, ani o tym, że elementy są zwarte w zbiorze kilka razy. Np. każdy z zapisów
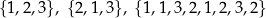
oznacza dokładnie ten sam zbiór.
4. Poprzez własności elementów. Bardzo wygodnym i uniwersalnym sposobem definiowania zbiorów (szczególnie zbiorów liczbowych) jest definicja postaci
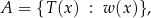
gdzie 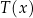 jest pewnym wyrażeniem (funkcją) zawierającym zmienną
jest pewnym wyrażeniem (funkcją) zawierającym zmienną  , a
, a 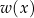 jest warunkiem jaki zmienna
jest warunkiem jaki zmienna  ma spełniać. Powyższą definicję czytamy:
ma spełniać. Powyższą definicję czytamy: 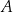 jest zbiorem tych elementów postaci
jest zbiorem tych elementów postaci 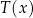 , które spełniają warunek
, które spełniają warunek 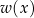 . Dwukropek czytamy: takich, że.
. Dwukropek czytamy: takich, że.
Zbiór
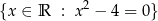
jest zbiorem (rzeczywistych) rozwiązań równania 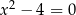 . (Czytamy: zbiór liczb rzeczywistych
. (Czytamy: zbiór liczb rzeczywistych  takich, że
takich, że 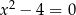 .)
.)
Zbiór
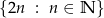
oznacza zbiór liczb naturalnych parzystych.
Przedziały liczbowe możemy zdefiniować następująco:
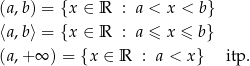
Powyższą notację możemy w naturalny sposób rozszerzyć na przypadek większej liczby zmiennych.
Zbiór
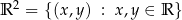
jest zbiorem par (uporządkowanych) liczb rzeczywistych. Poprzez wybór układu współrzędnych możemy ten zbiór utożsamiać z płaszczyzną.
Zbiór
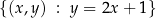
traktowany jako podzbiór płaszczyzny tworzy prostą. Zwykle ten zbiór definiujemy krótko mówiąc: prosta 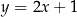 .
.
Zbiór
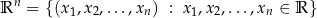
to zbiór wszystkich ciągów liczb rzeczywistych długości  . Jest to matematyczna definicja przestrzeni
. Jest to matematyczna definicja przestrzeni  wymiarowej.
wymiarowej.
Działania na zbiorach Zbiór 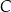 utworzony ze wszystkich elementów zbiorów
utworzony ze wszystkich elementów zbiorów 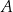 i
i 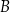 nazywamy sumą zbiorów
nazywamy sumą zbiorów 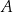 i
i 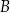 i oznaczamy
i oznaczamy
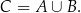
Zbiór 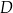 , który składa się z elementów należących jednocześnie do
, który składa się z elementów należących jednocześnie do 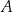 i do
i do 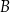 nazywamy częścią wspólną (lub przekrojem, lub też iloczynem) zbiorów
nazywamy częścią wspólną (lub przekrojem, lub też iloczynem) zbiorów 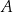 i
i 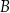 . Oznaczamy
. Oznaczamy
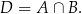
Jeżeli 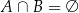 to mówimy, że zbiory
to mówimy, że zbiory 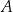 i
i 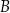 są rozłączne.
są rozłączne.
Zbiór 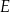 składający się z elementów zbioru
składający się z elementów zbioru 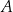 , które nie należą do
, które nie należą do 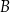 nazywamy różnicą zbiorów
nazywamy różnicą zbiorów 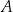 i
i 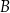 . Oznaczamy
. Oznaczamy
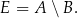
Jeżeli 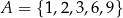 i
i 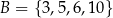 to
to
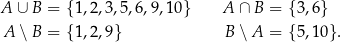
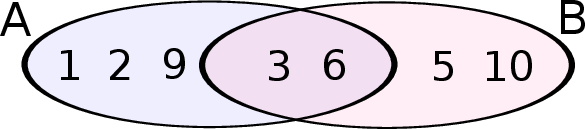
Jeżeli 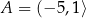 i
i 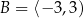 to
to
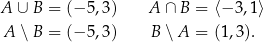

Jeżeli 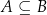 to
to 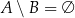
Jeżeli 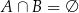 to
to 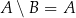 .
.
Bardzo wygodnym sposobem ilustracji zbiorów 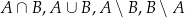 jest tzw. diagram Venna.
jest tzw. diagram Venna.
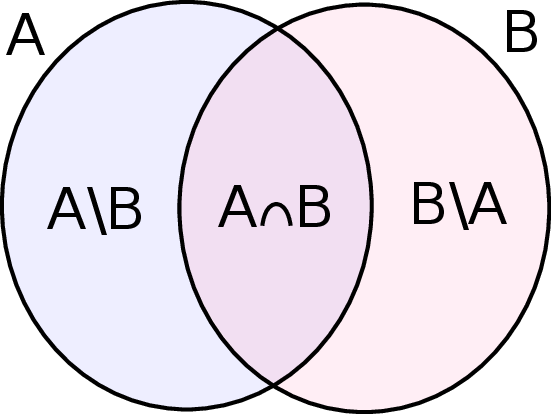
Diagram taki doskonale obrazuje wzajemne relacje między wymienionymi zbiorami i pozwala wymyślać różne przydatne wzorki, np.
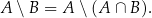
Kilka oczywistych wzorków.
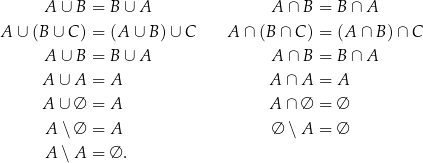
Dopełnienie i prawa de Morgana W pewnych sytuacjach zdarza się, że zbiory, którymi się zajmujemy są podzbiorami ustalonego zbioru 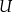 (o zbiorze
(o zbiorze 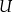 myślimy jak o przestrzeni, która zawiera wszystkie badane przez nas elementy). W takim kontekście definiujemy dopełnienie zbioru
myślimy jak o przestrzeni, która zawiera wszystkie badane przez nas elementy). W takim kontekście definiujemy dopełnienie zbioru 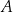 (w zbiorze
(w zbiorze 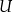 ) jako
) jako
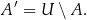
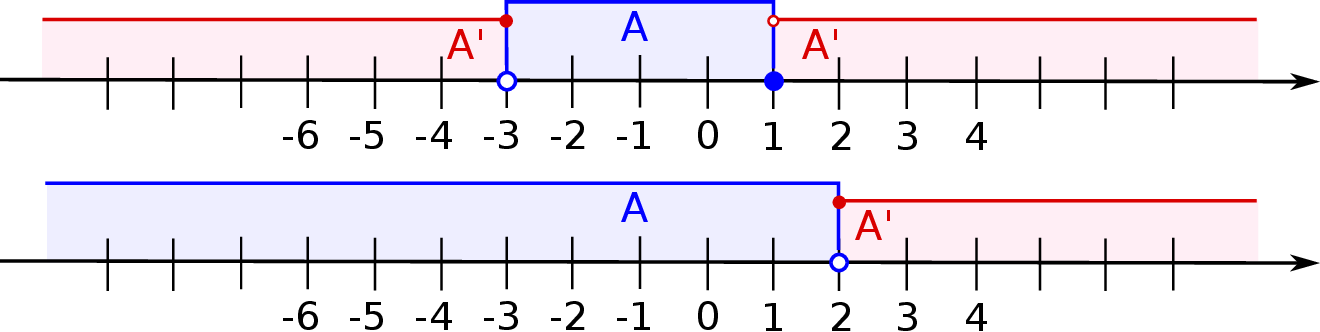
Przedziały liczbowe w naturalny sposób traktujemy jako podzbiory 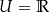 . Mamy zatem
. Mamy zatem
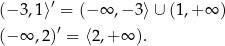
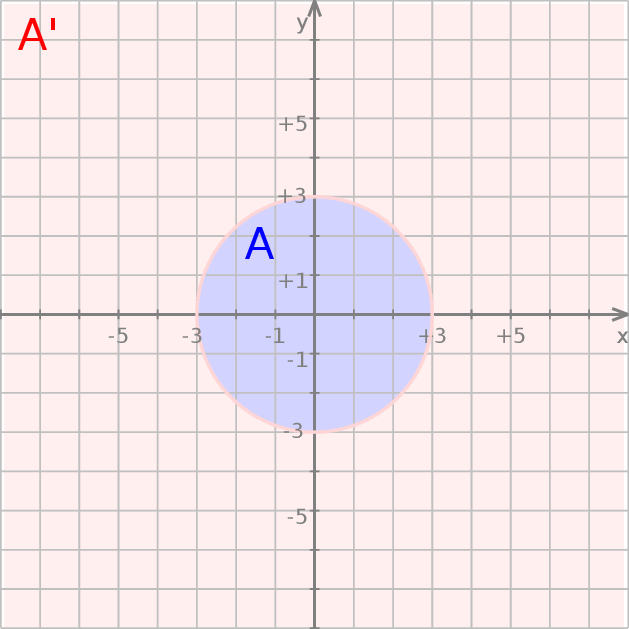
Podzbiory płaszczyzny w naturalny sposób traktujemy jako podzbiory płaszczyzny 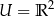 :) Zatem np.
:) Zatem np.
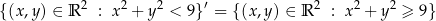
Poniższy obrazek
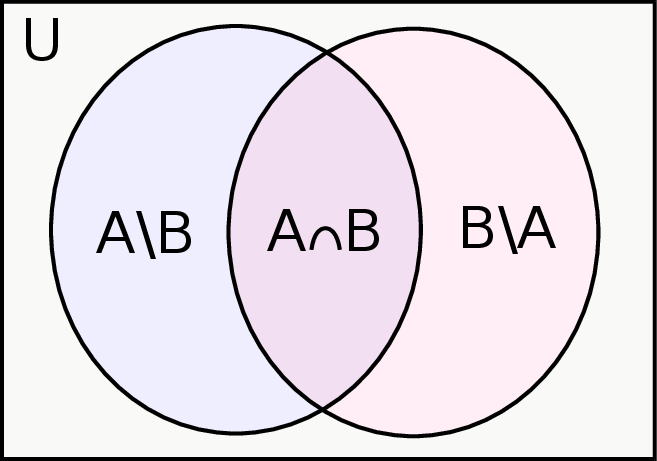
przedstawia diagram Venna uzupełniony o przestrzeń 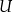 . Diagram ten jest bezcennym źródłem ciekawych wzorków, np.
. Diagram ten jest bezcennym źródłem ciekawych wzorków, np.
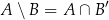
Dopełnienie odgrywa szczególną rolę, gdy zajmujemy się zdarzeniami losowymi. Jeżeli 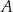 jest zdarzeniem losowym, a
jest zdarzeniem losowym, a 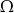 jest zbiorem zdarzeń elementarnych to zbiór
jest zbiorem zdarzeń elementarnych to zbiór
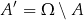
odpowiada zdarzeniu przeciwnemu do 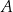 . W szczególności
. W szczególności
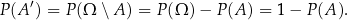
Kilka oczywistych wzorków.
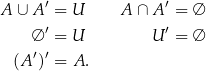
Używając diagramu Venna łatwo wykazać tzw. wzory (prawa) de Morgana.
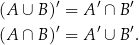
Prawa de Morgana są ciekawe, bo pozwalają zamieniać (przy pomocy dopełnienia) sumę na iloczyn i odwrotnie.
Iloczyn kartezjański Dla dowolnych zbiorów 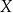 i
i 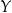 definiujemy ich iloczyn kartezjański wzorem
definiujemy ich iloczyn kartezjański wzorem
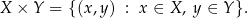
Mówiąc bardziej po ludzku, iloczyn kartezjański 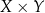 jest zbiorem wszystkich par (uporządkowanych) postaci
jest zbiorem wszystkich par (uporządkowanych) postaci 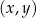 , gdzie
, gdzie  jest elementem zbioru
jest elementem zbioru 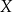 , a
, a 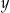 elementem zbioru
elementem zbioru 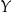 .
.
Jeżeli 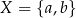 i
i 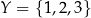 to
to
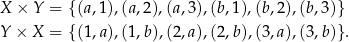
Zauważmy, że o elementach zbioru 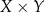 możemy myśleć jak o elementach tabelki.
możemy myśleć jak o elementach tabelki.

Analogicznie definiujemy iloczyn kartezjański większej liczby zbiorów 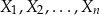
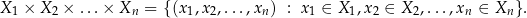
W szczególności jeżeli 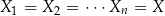 to oznaczamy
to oznaczamy
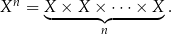
Zbiór 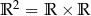 , czyli zbiór par liczb rzeczywistych utożsamiamy (poprzez wybór układu współrzędnych) z płaszczyzną.
, czyli zbiór par liczb rzeczywistych utożsamiamy (poprzez wybór układu współrzędnych) z płaszczyzną.
Zbiór 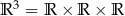 , czyli zbiór trójek liczb rzeczywistych utożsamiamy (poprzez wybór układu współrzędnych) z przestrzenią trójwymiarową.
, czyli zbiór trójek liczb rzeczywistych utożsamiamy (poprzez wybór układu współrzędnych) z przestrzenią trójwymiarową.
O zbiorze 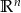 myślimy (poprzez analogię z
myślimy (poprzez analogię z 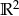 i
i 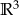 ) jak o przestrzeni
) jak o przestrzeni  wymiarowej.
wymiarowej.
Jeżeli przez 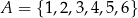 oznaczymy zbiór możliwych wyników przy jednokrotnym rzucie kostką, to zbiór możliwych wyników przy
oznaczymy zbiór możliwych wyników przy jednokrotnym rzucie kostką, to zbiór możliwych wyników przy  -krotnym rzucie kostką jest równy
-krotnym rzucie kostką jest równy 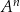 .
.
O zbiorze 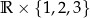 myślimy jak o zbiorze trzech kopii
myślimy jak o zbiorze trzech kopii 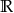 umieszczonych na poziomach 1, 2, 3.
umieszczonych na poziomach 1, 2, 3.
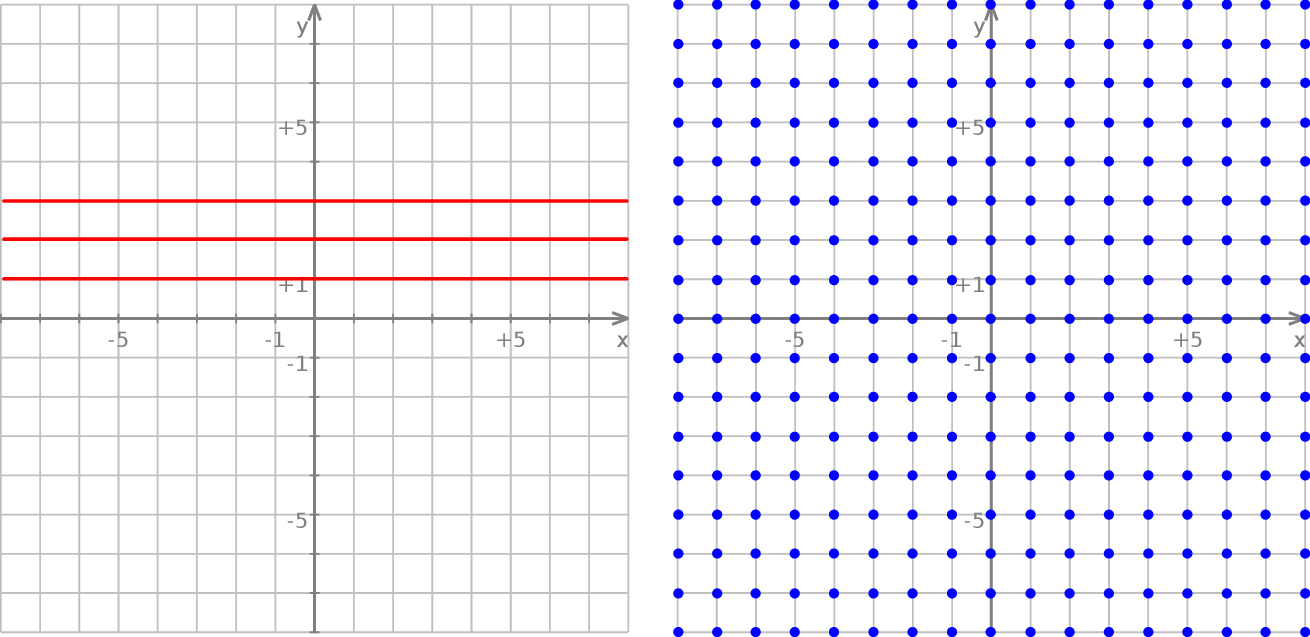
Jeżeli 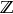 oznacza zbiór liczb całkowitych to zbiór
oznacza zbiór liczb całkowitych to zbiór 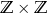 jest zbiorem punktów płaszczyzny, które mają obie współrzędne całkowite. Są to tzw. punkty kratowe.
jest zbiorem punktów płaszczyzny, które mają obie współrzędne całkowite. Są to tzw. punkty kratowe.
Liczba elementów Jeżeli 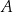 jest zbiorem skończonym, to symbolem
jest zbiorem skończonym, to symbolem
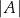
oznaczamy liczbę elementów zbioru 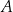 .
.
Np.
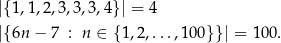
Patrząc na diagram Venna dla dwóch zbiorów skończonych 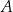 i
i 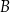 łatwo przekonać się o prawdziwości wzorów
łatwo przekonać się o prawdziwości wzorów
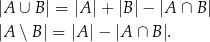
Jeżeli 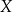 i
i 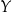 są zbiorami skończonymi to
są zbiorami skończonymi to
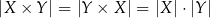
Tak jest, bo zbiór 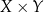 składa się z par, których pierwszy element może być wybrany na
składa się z par, których pierwszy element może być wybrany na 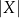 , a drugi na
, a drugi na 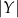 sposobów.
sposobów.
Inny sposób myślenia o tym wzorze: zbiór 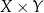 możemy utożsamiać z tabelką, która ma
możemy utożsamiać z tabelką, która ma 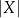 wierszy i
wierszy i 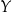 kolumn.
kolumn.

