Zadanie nr 2781720
Rzucamy cztery razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że suma kwadratów liczb oczek otrzymanych we wszystkich czterech rzutach będzie mniejsza niż 20.
Rozwiązanie
Za zdarzenia elementarne przyjmujemy czteroelementowe ciągi otrzymanych liczb oczek. Mamy więc
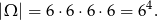
Zastanówmy się teraz, na ile sposobów suma kwadratów oczek może być mniejsza od 20.
Powyższe możliwości dzielą się na kilka typów. W przypadku rozkładów V i IX mamy po jednym zdarzeniu sprzyjającym
W przypadkach I, IV, VI, VIII mamy po 4 możliwości (bo na 4 sposoby możemy umieścić liczbę inną od pozostałych trzech).
W przypadku VII miejsca dla 2-jek możemy wybrać na
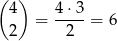
sposobów, a na pozostałych miejscach umieszczamy jedynki.
Pozostały przypadki II i III. Są one analogiczne, więc przeprowadzimy rachunek dla przypadku II. Miejsce dla 3-ki wybieramy na 4 sposoby, potem na 3 sposoby umieszczamy 1-kę, a na koniec na pozostałych dwóch miejscach umieszczamy 2-ki. W przypadkach II i III jest więc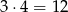 
możliwości. W sumie jest więc
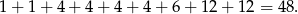
zdarzeń sprzyjających i prawdopodobieństwo jest równe
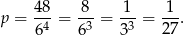
Odpowiedź: 
