/Szkoła średnia/Prawdopodobieństwo

Zadanie nr 2897848

Dodaj do ulubionych
Dodaj do rozwiązanych

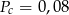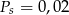Przy produkcji pewnego wyrobu wykonuje się dwie kolejno następujące po sobie operacje: cięcie i szlifowanie. Prawdopodobieństwa uszkodzenia obrabianego elementu w każdej z tych operacji wynoszą odpowiednio Pc = 0,08 i Ps = 0,02 .

  • Oblicz prawdopodobieństwo, że podany obróbce element zostanie uszkodzony.
  • Ile powinno wynosić prawdopodobieństwo 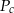Pc by prawdopodobieństwo uszkodzenia elementu w trakcie obróbki wynosiło mniej niż 0,069?

Rozwiązanie

Wprawdzie nie jest to podane w treści zadania, ale musimy założyć, że operacje te są niezależne (co zresztą wcale nie jest oczywiste – jak maszyna źle przytnie, to pewnie szanse na złe oszliwowanie są większe). Ponadto zakładamy, że źle przycięte przedmioty są mimo wszystko szlifowane (co też nie jest oczywiste).

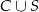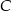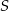  • Intersuje nas zdarzenie C ∪ S , gdzie C i S to zdarzenia popsucia elementu przy cięciu i szlifowaniu odpowiednio. Ze wzoru na prawdopodobieństwo sumy i z niezależności mamy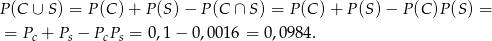
    P(C ∪ S ) = P(C )+ P(S )− P (C ∩ S) = P (C )+ P (S) − P(C )P(S ) = = Pc + Ps − PcPs = 0,1 − 0,00 16 = 0,098 4.

     
    Odpowiedź: 0,0984

  • Ze wzoru wyprowadzonego w poprzednim podpunkcie mamy nierówność.
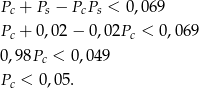
    Pc + Ps − PcPs < 0,069 Pc + 0,02 − 0,02Pc < 0,069 0,98Pc < 0,049 Pc < 0,05 .

     
    Odpowiedź: Pc < 0,05

Wersja PDF