/Szkoła średnia/Prawdopodobieństwo

Zadanie nr 2904984

Dodaj do ulubionych
Dodaj do rozwiązanych

Pogotowie ratunkowe dysponuje pewną liczbą karetek. W ciągu kilku miesięcy pracy stwierdzono, że w ciągu doby dana karetka będzie na miejscu w bazie z prawdopodobieństwem 0,4 jednakowym dla każdej karetki. Oblicz, ile karetek musi mieć do dyspozycji pogotowie, aby w razie wypadku, prawdopodobieństwo tego, że co najmniej jedna karetka jest na miejscu w bazie, było większe od 0,9.

Rozwiązanie

Opisaną sytuację dobrze opisuje schemat Bernoulliego. Jeżeli mamy n karetek i za sukces uważamy, że karetka jest w bazie, to pytanie jest o prawdopodobieństwo co najmniej jednego sukcesu przy n próbach. Oczywiście łatwiej jest obliczyć prawdopodobieństwo zdarzenia przeciwnego, czyli zdarzenia, że bazie nie ma żadnej karetki (0 sukcesów). Mamy zatem nierówność

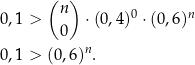
( ) 0,1 > n ⋅(0,4 )0 ⋅(0,6)n 0 0,1 > (0,6)n.

Sposób I

Łatwo teraz sprawdzić na kalkulatorze, że

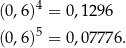
(0,6)4 = 0 ,1296 5 (0,6) = 0 ,07776.

Funkcja 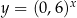x y = (0 ,6) jest malejąca, więc interesująca nas nierówność jest spełniona jeżeli n ≥ 5 .

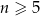Sposób II

Rozwiązujemy otrzymaną nierówność.

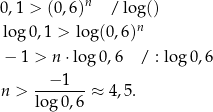
n 0,1 > (0,6) / log() lo g0,1 > lo g(0,6)n − 1 > n ⋅log 0,6 / : lo g0 ,6 --−-1-- n > log 0,6 ≈ 4,5 .

Po drodze zmieniliśmy znak nierówności, bo 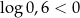log 0,6 < 0 .  
Odpowiedź: Co najmniej 5.

Wersja PDF