/Szkoła średnia/Prawdopodobieństwo

Zadanie nr 3083491

Dodaj do ulubionych
Dodaj do rozwiązanych

Danych jest 5 pudełek ponumerowanych liczbami od 1 do 5. W każdym pudełku znajduje się 20 kul ponumerowanych liczbami od 1 do 20. Z każdego pudełka wybieramy jedną kulę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że każda z wylosowanych liczb jest mniejsza od wszystkich liczb wylosowanych z pudełek o większych numerach. Wynik podaj w postaci ułamka nieskracalnego.

Rozwiązanie

Ustalmy najpierw o co chodzi. Liczba wylosowana z pierwszego pudełka musi być mniejsza od liczb wylosowanych z pudełek o numerach 2,3,4,5, liczba wylosowana z pudełka numer 2 musi być mniejsza od liczb wylosowanych z pudełek 3,4,5 itd. Jeżeli więc zapiszemy liczby wylosowane z kolejnych pudełek jako ciąg 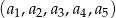(a1,a2,a3,a4,a5) to w zdarzeniach sprzyjających musi być spełniony warunek

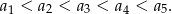
a1 < a 2 < a3 < a4 < a5.

Wszystkich zdarzeń elementarnych jest

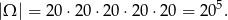
5 |Ω | = 20 ⋅20⋅ 20⋅ 20⋅2 0 = 20 .

Obliczmy teraz ile jest zdarzeń sprzyjających. Jak ustaliliśmy, musimy obliczyć, ile spośród tych ciągów jest rosnących. Każdy taki ciąg jest jednoznacznie wyznaczony przez 5 różnych liczb ze zbioru 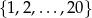{1,2,...,20} (bo kolejność tych liczb jest jednoznacznie ustalona). Zdarzeń sprzyjających jest więc

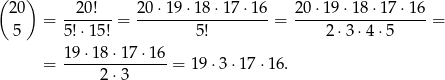
( 20) 20! 20⋅1 9⋅18 ⋅17 ⋅16 20 ⋅19 ⋅18 ⋅17⋅ 16 = ------- = ------------------= ------------------ = 5 5 !⋅15! 5! 2 ⋅3 ⋅4⋅5 1 9⋅18 ⋅17 ⋅16 = -----2-⋅3----- = 19 ⋅3⋅1 7⋅1 6.

Prawdopodobieństwo jest więc równe

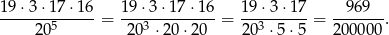
19⋅3 ⋅17 ⋅16 19 ⋅3⋅ 17⋅ 16 1 9⋅3 ⋅17 969 -------------= ------------- = --------- = -------. 20 5 203 ⋅20⋅ 20 203 ⋅5 ⋅5 2000 00

 
Odpowiedź: 209069000

Wersja PDF