/Szkoła średnia/Prawdopodobieństwo

Zadanie nr 3434651

Dodaj do ulubionych
Dodaj do rozwiązanych

Tomek i Romek postanowili rozegrać między sobą pięć partii szachów. Prawdopodobieństwo wygrania pojedynczej partii przez Tomka jest równe 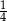14 . Oblicz prawdopodobieństwo wygrania przez Tomka co najmniej czterech z pięciu partii. Wynik podaj w postaci ułamka zwykłego nieskracalnego.

Rozwiązanie

Zadanie możemy rozwiązać przy pomocy schematu Bernoulliego. Pojedyncza próba to jedna partia szachów. Prawdopodobieństwo sukcesu w takiej próbie (czyli prawdopodobieństwo wygranej Tomka) wynosi 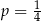p = 14 . Zatem prawdopodobieństwo uzyskania co najmniej 4 sukcesów w 5 próbach to

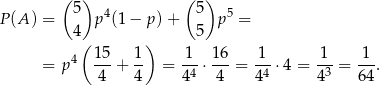
( ) ( ) 5 4 5 5 P(A ) = p (1 − p) + p = 4( ) 5 4 15- 1- 1-- 16- 1-- -1- -1- = p 4 + 4 = 44 ⋅ 4 = 44 ⋅4 = 4 3 = 64 .

 
Odpowiedź: -1 64

Wersja PDF