/Szkoła średnia/Prawdopodobieństwo

Zadanie nr 3480959

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz prawdopodobieństwo, że w dziesięciu rzutach kostką dokładnie na dwóch kostkach otrzymamy ściankę z dwoma oczkami i dokładnie na trzech kostkach ściankę z trzema oczkami.

Rozwiązanie

Za zdarzenia elementarne przyjmujemy ciągi otrzymanych liczb oczek. Zatem

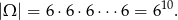
|Ω | = 6 ⋅6 ⋅6⋅⋅⋅6 = 610.

Liczymy ile jest zdarzeń sprzyjających. Kostki na których mają być dwa oczka możemy wybrać na

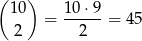
( ) 10 10-⋅9- 2 = 2 = 45

sposobów. Z pozostałych 8 kostek wybieramy 3, na których mają być trzy oczka. Możemy to zrobić na

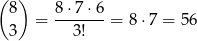
( 8) 8 ⋅7 ⋅6 = ------- = 8 ⋅7 = 5 6 3 3!

sposobów. Na pozostałych 5 kostkach liczba oczek może być równa 1, 4, 5 lub 6. W sumie jest więc

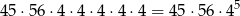
4 5⋅5 6⋅4 ⋅4 ⋅4⋅ 4⋅4 = 45⋅5 6⋅4 5

możliwości. Prawdopodobieństwo jest więc równe

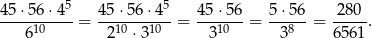
45⋅ 56⋅4 5 45 ⋅56 ⋅45 45⋅ 56 5 ⋅56 280 ----------= ---------- = -------= ------= -----. 610 210 ⋅310 310 38 656 1

 
Odpowiedź: 6258601

Wersja PDF