/Szkoła średnia/Prawdopodobieństwo

Zadanie nr 3720752

Dodaj do ulubionych
Dodaj do rozwiązanych

Liczba uczniów w klasie jest 812 razy mniejsza od liczby utworzonych z nich uporządkowanych trójek. Oblicz prawdopodobieństwo wylosowania trzech osób, które (w kolejności losowania) są zapisane w dzienniku pod numerami pierwszym, drugim, i trzecim.

Rozwiązanie

Powiedzmy, że uczniów jest n . Zatem uporządkowanych trójek uczniów jest

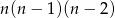
n(n − 1)(n− 2)

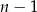(pierwszego ucznia możemy wybrać na n , drugiego na n − 1 , a trzeciego na 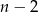n − 2 sposobów). Mamy więc równanie

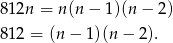
812n = n(n − 1 )(n− 2) 812 = (n− 1)(n − 2).

Można to równanie rozwiązać 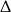Δ -ą, ale można też zgadnąć rozwiązanie: wystarczy zauważyć, że

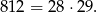
81 2 = 28 ⋅29.

Zatem 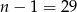n − 1 = 2 9 , czyli n = 30 .

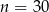Zajmijmy się teraz prawdopodobieństwem. Za zdarzenia sprzyjające przyjmujemy uporządkowane trójki wylosowanych osób, więc

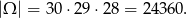
|Ω | = 3 0⋅2 9⋅28 = 24360.

Jest dokładnie jedno zdarzenie sprzyjające, więc szukane prawdopodobieństwo jest równe

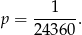
1 p = ------. 243 60

 
Odpowiedź: 241360

Wersja PDF