/Szkoła średnia/Prawdopodobieństwo

Zadanie nr 3789462

Dodaj do ulubionych
Dodaj do rozwiązanych

Z talii 52 kart wylosowano dwie karty i, nie oglądając ich, włożono do drugiej talii. W ten sposób powstała talia złożona z 54 kart. Oblicz prawdopodobieństwo wylosowania asa z tak utworzonej talii kart.

Rozwiązanie

Sposób I

Mamy trzy możliwości: albo do talii dołożyliśmy dwa asy, albo dołożyliśmy jednego asa, albo nie dołożyliśmy żadnego asa. Jeżeli oznaczymy te zdarzenia przez 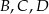B ,C ,D to mamy

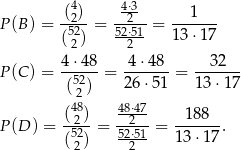
(42)- -4⋅32-- ---1--- P (B) = 52 = 52⋅51 = 13 ⋅17 (2) 2 4⋅-48- -4-⋅48- --32--- P (C) = 52 = 2 6⋅51 = 13 ⋅17 ( 2) (428) 48⋅247 188 P (D ) = -52- = -52⋅51 = -------. (2 ) 2 1 3⋅17

Jeżeli oznaczymy przez 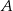A zdarzenie wylosowania asa z nowej talii, to ze wzoru na prawdopodobieństwo całkowite (lub z drzewka) mamy

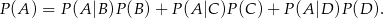
P (A ) = P(A |B)P (B) + P (A|C )P(C )+ P(A |D )P(D ).

Obliczmy powyższe prawdopodobieństwa warunkowe.

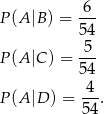
6 P(A |B) = --- 54 P(A |C) = 5-- 54 -4- P(A |D ) = 54 .

Mamy zatem

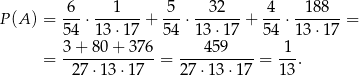
6-- ---1--- 5-- --32--- -4- -188--- P (A) = 54 ⋅13 ⋅17 + 54 ⋅13 ⋅17 + 5 4 ⋅ 13 ⋅17 = 3+ 80 + 376 45 9 1 = -------------= -----------= --. 27 ⋅13 ⋅17 27 ⋅13 ⋅17 13

Sposób II

Otrzymany wynik każe się zastanowić, czy nie ma prostszego sposobu wyliczenia tego prawdopodobieństwa. Oczywiście jest.

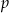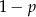O całej historii możemy myśleć następująco: mamy dwie talie i losujemy z nich jedną kartę (w końcu wylosowana karta jest z jednej lub z drugiej talii). Prawdopodobieństwa tego, że wyjmiemy kartę z pierwszej talii lub, że wyjmiemy z drugiej nie są równe (to odpowiada temu przekładaniu dwóch kart z pierwszej talii do drugiej). Nie jest jednak ważne ile wynoszą powiedzmy, że p i 1 − p . Ważne natomiast jest to, że wylosowanie asa z każdej talii ma prawdopodobieństwo 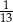113 . Ze wzoru na prawdopodobieństwo całkowite mamy

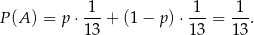
P (A ) = p ⋅-1-+ (1 − p )⋅-1- = -1-. 13 1 3 1 3

 
Odpowiedź: 113

Wersja PDF