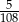/Szkoła średnia/Prawdopodobieństwo

Zadanie nr 3869402

Dodaj do ulubionych
Dodaj do rozwiązanych

Rzucamy cztery razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że iloczyn liczb oczek otrzymanych we wszystkich czterech rzutach będzie równy 60 .

Rozwiązanie

Z zdarzenia elementarne przyjmujemy czteroelementowe ciągi otrzymanych liczb oczek. Mamy więc

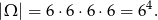
|Ω | = 6⋅6 ⋅6 ⋅6 = 64.

Zastanówmy się teraz na ile sposobów 60 może być napisane jako iloczyn czterech liczb oczek. Łatwo ustalić, że są trzy możliwości:

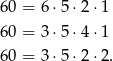
60 = 6⋅5 ⋅2 ⋅1 60 = 3⋅5 ⋅4 ⋅1 60 = 3⋅5 ⋅2 ⋅2.

Pierwszym dwóm sytuacjom odpowiada

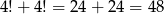
4!+ 4 ! = 2 4+ 2 4 = 48

zdarzeń elementarnych. Obliczmy ile jest zdarzeń odpowiadających trzeciej sytuacji. Miejsce dla 3-ki możemy wybrać na 4 sposoby, miejsce dla 5-ki na 3 sposoby i wtedy na pozostałych miejscach umieszczamy 2-ki. Jest więc 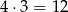4 ⋅3 = 12 zdarzeń sprzyjających tego typu i prawdopodobieństwo jest równe

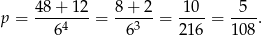
p = 48-+-12-= 8+--2-= 10--= -5-. 6 4 63 216 108

 
Odpowiedź: -5- 108

Wersja PDF