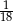/Szkoła średnia/Prawdopodobieństwo

Zadanie nr 4086824

Dodaj do ulubionych
Dodaj do rozwiązanych

Rzucamy dwa razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo każdego z następujących zdarzeń:

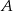  • A — w każdym rzucie wypadnie nieparzysta liczba oczek.
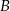  • B -– suma oczek otrzymanych w obu rzutach jest liczbą większą od 9.
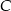  • C -– suma oczek otrzymanych w obu rzutach jest liczbą nieparzystą i większą od 9.

Rozwiązanie

Za zdarzenia elementarne przyjmijmy uporządkowane pary wyrzuconych oczek. Zatem

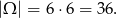
|Ω | = 6 ⋅6 = 36 .
  • Zdarzeń sprzyjających jest 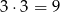3 ⋅3 = 9 (i za pierwszym i za drugim razem mamy 3 możliwości). Zatem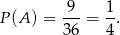
    9 1 P (A ) = ---= -. 36 4

     
    Odpowiedź: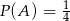 P(A ) = 14

  • Wypiszmy zdarzenia sprzyjające
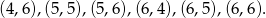
    (4,6 ),(5 ,5),(5,6),(6,4),(6,5),(6,6).

    Jest ich 6, zatem

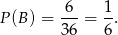
    6 1 P (B) = ---= -. 36 6

     
    Odpowiedź: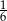 1 6

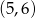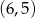  • Spośród zdarzeń wypisanych w poprzednim podpunkcie tylko (5,6) i (6,5) spełniają podany warunek. Zatem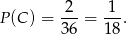
    -2- -1- P(C ) = 36 = 18 .

     
    Odpowiedź: 1 18

Wersja PDF