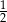Zadanie nr 4405654
Ze zbioru 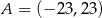 losujemy dwucyfrową liczbę całkowitą
losujemy dwucyfrową liczbę całkowitą  , natomiast ze zbioru
, natomiast ze zbioru 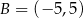 losujemy liczbę całkowitą
losujemy liczbę całkowitą 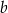 . Te liczby są współczynnikami funkcji
. Te liczby są współczynnikami funkcji 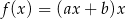 . Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wykres otrzymanej funkcji
. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wykres otrzymanej funkcji 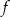 ma co najmniej dwa punkty wspólne z prostą
ma co najmniej dwa punkty wspólne z prostą 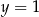 .
.
Rozwiązanie
Liczby całkowite w zbiorach 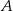 i
i 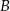 to odpowiednio
to odpowiednio
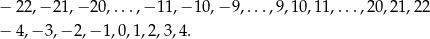
W takim razie parę liczb całkowitych 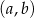 taką, że
taką, że 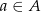 ,
, 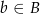 i
i  dwucyfrowa możemy wybrać na
dwucyfrowa możemy wybrać na
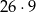
sposobów. Pozostało teraz ustalić dla ilu par 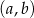 funkcja
funkcja
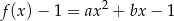
ma co najmniej dwa miejsca zerowe. Aby tak było musi być oczywiście 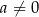 oraz
oraz
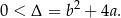
Zauważmy, że jeżeli 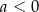 , to automatycznie
, to automatycznie 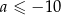 , czyli
, czyli 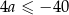 . Wtedy jednak nie uda nam się dobrać
. Wtedy jednak nie uda nam się dobrać 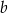 , bo
, bo 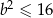 . Odwrotnie, jeżeli
. Odwrotnie, jeżeli 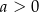 , to automatycznie
, to automatycznie
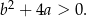
W takim razie jest
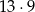
par, dla których parabola 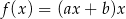 ma co najmniej dwa punkty wspólne z prostą
ma co najmniej dwa punkty wspólne z prostą 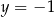 i interesujące nas prawdopodobieństwo jest równe
i interesujące nas prawdopodobieństwo jest równe
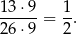
Odpowiedź: