Zadanie nr 4661355
Spośród liczb: -9, -7, -5, -3, -1, 0, 2, 4, 6, 8 losujemy dwie różne liczby  i
i 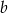 , a następnie zapisujemy ich iloczyn
, a następnie zapisujemy ich iloczyn 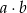 . Oblicz i porównaj prawdopodobieństwa zdarzeń
. Oblicz i porównaj prawdopodobieństwa zdarzeń 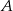 i
i 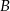 , jeśli:
, jeśli: 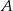 oznacza zdarzenie, że iloczyn
oznacza zdarzenie, że iloczyn 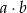 jest liczbą nieujemną;
jest liczbą nieujemną; 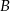 – zdarzenie, że iloczyn
– zdarzenie, że iloczyn 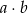 jest liczbą niedodatnią.
jest liczbą niedodatnią.
Rozwiązanie
Sposób I
Przyjmijmy za przestrzeń zdarzeń elementarnych 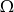 wszystkie możliwe pary
wszystkie możliwe pary 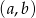 wylosowanych liczb (uwzględniamy kolejność). Wszystkich takich par jest
wylosowanych liczb (uwzględniamy kolejność). Wszystkich takich par jest 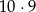 (pierwszą liczbę wybieramy dowolnie, drugą z pozostałych dziewięciu). Zatem
(pierwszą liczbę wybieramy dowolnie, drugą z pozostałych dziewięciu). Zatem
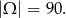
Zdarzenia sprzyjające do 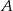 możemy podzielić na
możemy podzielić na
- jedna z wylosowanych liczb jest 0, druga dowolna – takich zdarzeń jest 9+9=18
- pierwsza wylosowana liczba jest ujemna, druga też ujemna –
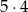 zdarzeń
zdarzeń - pierwsza wylosowana liczba jest dodatnia, druga też dodatnia –
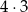 zdarzeń
zdarzeń
Zatem
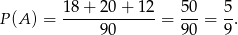
Podobnie wyliczamy prawdopodobieństwo zdarzenia 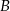
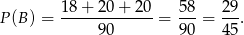
Sposób II
Tym razem przyjmijmy, że 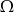 składa się z par
składa się z par 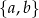 , gdzie nie uwzględniamy kolejności (czyli tak naprawdę mamy podzbiory dwuelementowe). Wszystkich takich podzbiorów jest
, gdzie nie uwzględniamy kolejności (czyli tak naprawdę mamy podzbiory dwuelementowe). Wszystkich takich podzbiorów jest 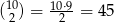 . Zatem
. Zatem
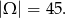
Podobnie jak poprzednio, zdarzenia sprzyjające do 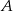 dzielimy na
dzielimy na
- Jedna z wylosowanych liczb to 0, druga dowolna – jest 9 takich zdarzeń.
- Obie liczby są dodatnie –
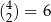 możliwości.
możliwości. - Obie liczby są ujemne –
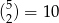 możliwości.
możliwości.
Mamy zatem
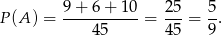
Zdarzenia sprzyjające do 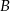 są dwóch rodzajów
są dwóch rodzajów
- Jedna z wylosowanych liczb to 0, druga dowolna – jest 9 takich zdarzeń.
- Jedna liczba jest dodatnia, druga ujemna – jest
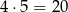 takich zdarzeń.
takich zdarzeń.
Zatem
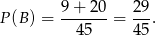
Odpowiedź: